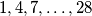
Deset brojeva (razlika dvaju uzastopnih je ) raspoređeno je u krug. Sa označimo najveću od deset suma koje dobivamo tako da svaki od brojeva zbrojimo s dva njemu susjedna broja. Koja je najmanja vrijednost broja koju možemo postići?
%V0
Deset brojeva $1, 4, 7, \ldots, 28$ (razlika dvaju uzastopnih je $3$) raspoređeno je u krug. Sa $N$ označimo najveću od deset suma koje dobivamo tako da svaki od brojeva zbrojimo s dva njemu susjedna broja. Koja je najmanja vrijednost broja $N$ koju možemo postići?
Školjka 
(razlika dvaju uzastopnih je 
) raspoređeno je u krug. Sa 
označimo najveću od deset suma koje dobivamo tako da svaki od brojeva zbrojimo s dva njemu susjedna broja. Koja je najmanja vrijednost broja