Državno natjecanje 2013 SŠ3 3
Dodao/la:
arhiva12. srpnja 2013. Dokaži da je među bilo koja četiri broja iz intervala
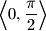
moguće odabrati dva broja, nazovimo ih

i

, tako da vrijedi
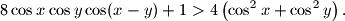
%V0
Dokaži da je među bilo koja četiri broja iz intervala $\displaystyle \left\langle 0,\frac{\pi}{2} \right\rangle$ moguće odabrati dva broja, nazovimo ih $x$ i $y$, tako da vrijedi $$8\cos x\cos y\cos(x-y)+1>4\left(\cos^2 x+\cos^2 y\right).$$
Izvor: Državno natjecanje iz matematike 2013