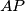
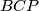
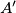
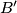
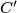
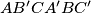
Neka je trokut sa stranicama duljina , i i neka je točka u njegovoj unutrašnjosti. Neka pravac ponovno siječe kružnicu opisanu trokutu u točki i neka su i točke definirane analogno. Dokaži da za opseg šesterokuta vrijedi
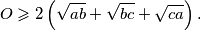
%V0
Neka je $ABC$ trokut sa stranicama duljina $a$, $b$ i $c$ i neka je $P$ točka u njegovoj unutrašnjosti. Neka pravac $AP$ ponovno siječe kružnicu opisanu trokutu $BCP$ u točki $A'$ i neka su $B'$ i $C'$ točke definirane analogno. Dokaži da za opseg $O$ šesterokuta $AB'CA'BC'$ vrijedi $$ O \geqslant 2 \left(\sqrt{ab} + \sqrt{bc} + \sqrt{ca}\right) \text{.} $$
Školjka 
trokut sa stranicama duljina 
, 
i 
i neka je 
točka u njegovoj unutrašnjosti. Neka pravac 
ponovno siječe kružnicu opisanu trokutu 
u točki 
i neka su 
i 
točke definirane analogno. Dokaži da za opseg 
šesterokuta 
vrijedi 