Državno natjecanje 2010 SŠ3 4
Dodao/la:
arhiva1. travnja 2012. Odredi sve prirodne brojeve
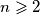
takve da za proizvoljne pozitivne realne brojeve

,
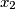
, ...,
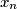
vrijedi nejednakost:
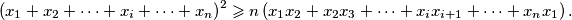
%V0
Odredi sve prirodne brojeve $n \geqslant 2$ takve da za proizvoljne pozitivne realne brojeve $x_1$, $x_2$, ..., $x_n$ vrijedi nejednakost: $$ \left(x_1+x_2+\cdots + x_i + \cdots + x_n\right)^2 \geqslant n\left(x_1x_2 + x_2x_3 + \cdots + x_ix_{i+1}+ \cdots + x_nx_1\right) \text{.} $$
Izvor: Državno natjecanje iz matematike 2010