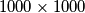
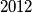
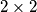
Svako polje ploče obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat koji sadrži tri polja jedne boje i jedno polje druge boje.
%V0
Svako polje ploče $1000 \times 1000$ obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za $2012$ veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat $2 \times 2$ koji sadrži tri polja jedne boje i jedno polje druge boje.
Školjka 
obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za 
veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat 
koji sadrži tri polja jedne boje i jedno polje druge boje.