Državno natjecanje 1995 SŠ4 1
Dodao/la:
arhiva1. travnja 2012. Zadan je trokut
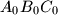
s kutovima
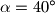
,
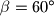
,
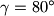
. Neka su

,

,

nožišta visina tog trouta. Na isti način se polazeći od trokuta
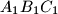
konstruira trokut
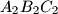
, zatim redom trokuti
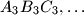
Dokažite da je trokut
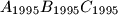
sličan trokutu
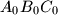
.
%V0
Zadan je trokut $A_0B_0C_0$ s kutovima $\alpha = 40^\circ$, $\beta = 60^\circ$, $\gamma = 80^\circ$. Neka su $A_1$, $B_1$, $C_1$ nožišta visina tog trouta. Na isti način se polazeći od trokuta $A_1B_1C_1$ konstruira trokut $A_2B_2C_2$, zatim redom trokuti $A_3B_3C_3,\ldots$ Dokažite da je trokut $A_{1995}B_{1995}C_{1995}$ sličan trokutu $A_0B_0C_0$.
Izvor: Državno natjecanje iz matematike 1995