Školjka

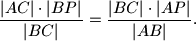
%V0 Unutar šiljastokutnog trokuta $ABC$ nalazi se točka $P$ takva da je $$\angle{APB}=\angle{CBA}+\angle{ACB}, \qquad \angle{BPC}=\angle{ACB}+\angle{BAC}.$$ Dokaži da vrijedi $$\frac{|AC|\cdot |BP|}{|BC|}=\frac{|BC|\cdot |AP|}{|AB|}.$$