IMO 2014 problem 1
Dodao/la:
arhiva21. rujna 2014. Let
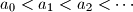
be an infinite sequence of positive integers. Prove that there exists a unique integer
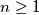
such that
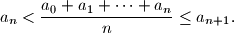
%V0
Let $a_0 < a_1 < a_2 < \cdots$ be an infinite sequence of positive integers. Prove that there exists a unique integer $n \geq 1$ such that $$
a_n < \frac{a_0 + a_1 + \cdots + a_n}{n} \leq a_{n+1} \text{.}
$$
Izvor: International Mathematical Olympiad 2014, day 1