IMO 2014 problem 3
Dodao/la:
arhiva21. rujna 2014. Convex quadrilateral

has
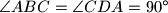
. Point

is the foot of the perpendicular from

to

. Points

to

lie on sides

and

, respectively, such that

lies inside triangle
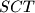
and

Prove that line

is tangent to the circumcircle of triangle
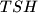
.
%V0
Convex quadrilateral $ABCD$ has $\angle ABC = \angle CDA = 90^\circ$. Point $H$ is the foot of the perpendicular from $A$ to $BD$. Points $S$ to $T$ lie on sides $AB$ and $AD$, respectively, such that $H$ lies inside triangle $SCT$ and $$
\angle CHS - \angle CSB = 90^\circ, \quad
\angle THC - \angle DTC = 90^\circ \text{.}
$$
Prove that line $BD$ is tangent to the circumcircle of triangle $TSH$.
Izvor: International Mathematical Olympiad 2014, day 1