IMO 2014 problem 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 For each positive integer  , the Bank of Cape Town issues coins of denomination
, the Bank of Cape Town issues coins of denomination 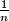 . Given a finite collection of such coins (of not necessarily different denominations) with total value at most
. Given a finite collection of such coins (of not necessarily different denominations) with total value at most 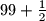 , prove that it is possible to split this collection into
, prove that it is possible to split this collection into 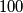 or fewer groups, such that each group has total value at most
or fewer groups, such that each group has total value at most 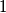 .
.
 , the Bank of Cape Town issues coins of denomination
, the Bank of Cape Town issues coins of denomination 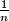 . Given a finite collection of such coins (of not necessarily different denominations) with total value at most
. Given a finite collection of such coins (of not necessarily different denominations) with total value at most 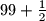 , prove that it is possible to split this collection into
, prove that it is possible to split this collection into 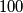 or fewer groups, such that each group has total value at most
or fewer groups, such that each group has total value at most 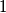 .
. Izvor: International Mathematical Olympiad 2014, day 2
 Školjka
Školjka 
