IMO 2014 problem 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 A set of line sin the plane is in general position if no two are parallel and no three pass through the same point. A set of lines in general position cuts the plane into regions, some of which have finite area; we call these its finite regions. Prove that for all sufficiently large  , in any set of
, in any set of  lines in general position it is possible to colour at least
lines in general position it is possible to colour at least 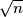 of the lines blue in such a way that none of its finite regions has a completely blue boundary.
of the lines blue in such a way that none of its finite regions has a completely blue boundary.
Note: Results with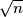 replaced by
replaced by 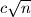 will be awarded points depending on the value of the constant
will be awarded points depending on the value of the constant  .
.
 , in any set of
, in any set of  lines in general position it is possible to colour at least
lines in general position it is possible to colour at least 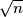 of the lines blue in such a way that none of its finite regions has a completely blue boundary.
of the lines blue in such a way that none of its finite regions has a completely blue boundary.Note: Results with
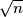 replaced by
replaced by 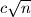 will be awarded points depending on the value of the constant
will be awarded points depending on the value of the constant  .
. Izvor: International Mathematical Olympiad 2014, day 2
 Školjka
Školjka 
