Državno natjecanje 2000 SŠ4 4
Dodao/la:
arhiva1. travnja 2012. Neka je
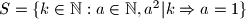
i

. Dokažite da je
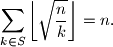
(
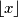
je oznaka za najveći cijeli broj koji nije veći od

.)
%V0
Neka je $S = \{k \in \mathbb{N} : a \in \mathbb{N}, a^2|k \Rightarrow a = 1 \}$ i $n \in \mathbb{N}$. Dokažite da je
$$\sum_{k \in S} \left\lfloor \sqrt{\frac{n}{k}} \right\rfloor = n.$$
( $\lfloor x \rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)
Izvor: Državno natjecanje iz matematike 2000