Županijsko natjecanje iz matematike 2015, SŠ4 A 4
Dodao/la:
arhiva22. ožujka 2015. Za prirodan broj kažemo da je emph{zvrkast} ako u dekadskom zapisu ima

znamenaka i ako uklanjanjem bilo koje njegove znamenke nastaje
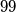
-znamenkasti broj djeljiv sa

.
Koliko ima zvrkastih prirodnih brojeva?
%V0
Za prirodan broj kažemo da je \emph{zvrkast} ako u dekadskom zapisu ima $100$ znamenaka i ako uklanjanjem bilo koje njegove znamenke nastaje $99$-znamenkasti broj djeljiv sa $7$.
Koliko ima zvrkastih prirodnih brojeva?
Izvor: Županijsko natjecanje iz matematike 2015