IMO 2015 zadatak 1
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 Konačan skup  točaka u ravnini je balansiran ako za bilo koje dvije različite točke
točaka u ravnini je balansiran ako za bilo koje dvije različite točke  i
i  u
u  postoji točka
postoji točka  u
u  takva da je
takva da je 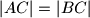 . Kažemo da je
. Kažemo da je  ekscentričan ako ni za koje tri u parovima različite točke
ekscentričan ako ni za koje tri u parovima različite točke  ,
,  i
i  u
u  ne postoji točka
ne postoji točka  u
u  takva da je
takva da je 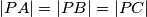 .
.
(a) Dokaži da za svaki prirodni broj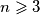 postoji balansirani skup koji se sastoji od
postoji balansirani skup koji se sastoji od  točaka.
točaka.
(b) Odredi sve prirodne brojeve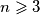 za koje postoji balansirani ekscentrični skup koji se sastoji od
za koje postoji balansirani ekscentrični skup koji se sastoji od  točaka.
točaka.
 točaka u ravnini je balansiran ako za bilo koje dvije različite točke
točaka u ravnini je balansiran ako za bilo koje dvije različite točke  i
i  u
u  postoji točka
postoji točka  u
u  takva da je
takva da je 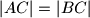 . Kažemo da je
. Kažemo da je  ekscentričan ako ni za koje tri u parovima različite točke
ekscentričan ako ni za koje tri u parovima različite točke  ,
,  i
i  u
u  ne postoji točka
ne postoji točka  u
u  takva da je
takva da je 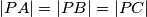 .
.(a) Dokaži da za svaki prirodni broj
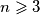 postoji balansirani skup koji se sastoji od
postoji balansirani skup koji se sastoji od  točaka.
točaka.(b) Odredi sve prirodne brojeve
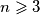 za koje postoji balansirani ekscentrični skup koji se sastoji od
za koje postoji balansirani ekscentrični skup koji se sastoji od  točaka.
točaka. Izvor: Međunarodna matematička olimpijada 2015, prvi dan
 Školjka
Školjka 
