IMO 2015 zadatak 5
Dodao/la:
arhiva14. srpnja 2015. Neka je
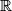
skup realnih brojeva. Odredi sve funkcije
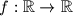
za koje vrijedi jednakosti
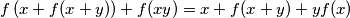
za sve realne brojeve

i

.
%V0
Neka je $\mathbb{R}$ skup realnih brojeva. Odredi sve funkcije $f : \mathbb{R} \to \mathbb{R}$ za koje vrijedi jednakosti $$
f\left(x + f(x + y) \right) + f(xy) = x + f(x + y) + y f(x)
$$ za sve realne brojeve $x$ i $y$.
Izvor: Međunarodna matematička olimpijada 2015, drugi dan