IMO 2015 zadatak 6
Dodao/la:
arhiva14. srpnja 2015. Niz
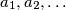
cijelih brojeva zadovoljava sljedeće uvjete:
(i)
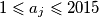
za sve
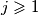
;
(ii)
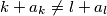
za sve
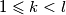
.
Dokaži da postoje prirodni brojevi

i

takvi da je
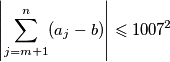
za sve cijele brojeve

i

koji zadovoljavaju
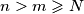
.
%V0
Niz $a_1, a_2, \ldots$ cijelih brojeva zadovoljava sljedeće uvjete:
(i) $1 \leqslant a_j \leqslant 2015$ za sve $j \geqslant 1$;
(ii) $k + a_k \neq l + a_l$ za sve $1 \leqslant k < l$.
Dokaži da postoje prirodni brojevi $b$ i $N$ takvi da je $$
\left| \sum_{j=m+1}^n (a_j - b) \right| \leqslant 1007^2
$$ za sve cijele brojeve $m$ i $n$ koji zadovoljavaju $n > m \geqslant N$.
Izvor: Međunarodna matematička olimpijada 2015, drugi dan