IMO 2016 zadatak 1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0Trokut 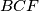 ima pravi kut u vrhu
ima pravi kut u vrhu  . Neka je
. Neka je  točka na pravcu
točka na pravcu 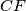 takva da je
takva da je 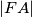 =
= 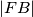 i da točka
i da točka  leži između točaka
leži između točaka  i
i  . Točka
. Točka  je izabrana tako da je
je izabrana tako da je 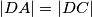 i da je pravac
i da je pravac  simetrala kuta
simetrala kuta 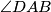 . Točka
. Točka  je izabrana tako da je
je izabrana tako da je 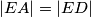 i da je pravac
i da je pravac  simetrala kuta
simetrala kuta 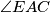 . Neka je točka
. Neka je točka  polovište dužine
polovište dužine 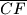 . Neka je točka
. Neka je točka  takva da je četverokut
takva da je četverokut 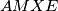 paralelogram
paralelogram 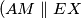 i
i 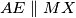 ). Dokaži da se pravci
). Dokaži da se pravci  ,
, 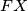 i
i 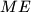 sijeku u jednoj točki.
sijeku u jednoj točki.
Izvor: Međunarodna matematička olimpijada 2016
 Školjka
Školjka 
