Školjka

U ravnini se nalazi 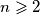$n \geqslant 2$ dužina takvih da se svake dvije dužine sijeku u unutrašnjoj točki i da nikoje tri dužine nemaju zajedničku točku. Geoff mora izabrati po jednu krajnju točku svake dužine i na nju postaviti žabu okrenutu prema drugoj krajnjoj točki te dužine. Potom će pljesnuti rukama $n-1$ puta. Svaki put kada pljesne, svaka žaba odmah skoči prema naprijed do iduće točke presjeka na svojoj dužini. Žabe nikad ne mijenjaju smjer svojih skokova. Geoffu želi postaviti žabe tako da nikoje dvije od njih niti u jednom trenutku ne zauzimaju istu točku presjeka. $a)$ Dokaži da Geoff uvijek može ispuniti svoju želju ako je $n$ neparan. $b)$ Dokaži da Geoff nikad ne može ispuniti svoju želju ako je $n$ paran.