IMO 2017 zadatak 4
Kvaliteta:
Avg: 4,0Težina:
Avg: 5,5Neka su  i
i  međusobno različite točke na kružnici
međusobno različite točke na kružnici  takve da
takve da 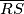 nije promjer. Neka je
nije promjer. Neka je  tangenta na kružnicu
tangenta na kružnicu  u točki
u točki  . Neka je
. Neka je  točka takva da je
točka takva da je  polovište dužine
polovište dužine 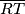 . Točka
. Točka 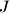 nalazi se na kraćem luku
nalazi se na kraćem luku 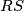 kružnice
kružnice  tako da se opisana kružnica
tako da se opisana kružnica  trokuta
trokuta 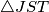 i pravac
i pravac  sijeku u dvije različite točke. Neka je
sijeku u dvije različite točke. Neka je  ono sjecište od
ono sjecište od  i
i  koje je bliže točki
koje je bliže točki  . Pravac
. Pravac 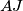 siječe kružnicu
siječe kružnicu  još u točki
još u točki  . Dokaži da pravac
. Dokaži da pravac 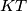 dodiruje kružnicu
dodiruje kružnicu  .
.
Izvor: Međunarodna matematička olimpijada 2017
 Školjka
Školjka 
