Školjka

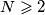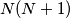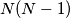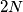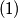Dan je prirodni broj $N \geqslant 2$. U skupini od $N(N+1)$ nogometaša nikoja dva nisu iste visine. Ri su nogometaši poredani u red. Trener želi iz reda izbaciti $N(N-1)$ igrača tako da preostalih $2N$ igrača tvori red za koji vrijedi sljedećih $N$ uvjeta: $\text{(1)}$ između dva najviša igrača nema nikoga, 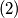$\text{(2)}$ između trećeg i četvrtog igrača po visini nema nikoga, 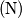$...$ $\text{(N)}$ između dva najniža igrača po visini nema nikoga. Dokaži da je to uvijek moguće napraviti.