Školsko/gradsko natjecanje iz matematike 2018, SŠ4 A 5
Dodao/la:
arhiva5. rujna 2018. Odredi geometrijsko mjesto (skup) središta svih kružnica koje izvana diraju kružnicu s jednadžbom 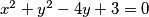 , a os
, a os  im je tangenta.
im je tangenta.
Odredi geometrijsko mjesto (skup) središta svih kružnica koje izvana diraju kružnicu s jednadžbom $x^2 +y^2 - 4y + 3=0$, a os $x$ im je tangenta.
Izvor: Školsko/gradsko natjecanje iz matematike 2018