IMO 2019 zadatak 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0Na stranicama  i
i  trokuta
trokuta  dane su točke
dane su točke  i
i  , redom. Neka su
, redom. Neka su  i
i  točke na dužinama
točke na dužinama 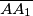 i
i 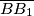 , redom, takve da su pravci
, redom, takve da su pravci  i
i  paralelni. Neka je
paralelni. Neka je 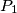 točka na pravcu
točka na pravcu 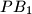 takva da točka
takva da točka  leži strogo između točaka
leži strogo između točaka  i
i 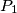 te da je
te da je 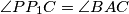 . Neka je
. Neka je 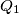 točka na pravcu
točka na pravcu 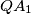 takva da točka
takva da točka  leži strogo između točaka
leži strogo između točaka  i
i 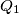 te da je
te da je 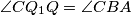 .
.
Dokaži da su točke  ,
,  ,
, 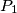 i
i 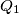 konciklične.
konciklične.
Izvor: Međunarodna matematička olimpijada 2019, problem 2
 Školjka
Školjka 
