IMO 2019 zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka društvena mreža ima 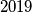 korisnika i neki parovi korisnika su prijatelji. Ako je
korisnika i neki parovi korisnika su prijatelji. Ako je  prijatelj korisniku
prijatelj korisniku  , onda je i
, onda je i  prijatelj korisniku
prijatelj korisniku  . Sljedeći događaji mogu se ponavljati jedan za drugim, ali ne istovremeno:
. Sljedeći događaji mogu se ponavljati jedan za drugim, ali ne istovremeno:
Tri korisnika  ,
,  i
i  , takva da su
, takva da su  i
i  prijatelji korisniku
prijatelji korisniku  , ali
, ali  i
i  nisu prijatelji, mijenjaju svoje statuse prijateljstava tako da su
nisu prijatelji, mijenjaju svoje statuse prijateljstava tako da su  i
i  sada prijatelji, ali
sada prijatelji, ali  više nije prijatelj korisniku
više nije prijatelj korisniku  , niti korisniku
, niti korisniku  . Svi ostali statusi prijateljstava ostaju nepromijenjeni.
. Svi ostali statusi prijateljstava ostaju nepromijenjeni.
Na početku, 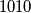 korisnika ima po
korisnika ima po 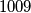 prijatelja i
prijatelja i 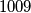 korisnika ima po
korisnika ima po 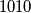 prijatelja. Dokaži da postoji niz opisanih događaja nakon kojega svaki korisnik ima najviše jednog prijatelja.
prijatelja. Dokaži da postoji niz opisanih događaja nakon kojega svaki korisnik ima najviše jednog prijatelja.
Izvor: Međunarodna matematička olimpijada 2019, problem 3
 Školjka
Školjka 
