IMO 2019 zadatak 5
Kvaliteta:
Avg: 5,0Težina:
Avg: 8,0Banka Batha izdaje kovanice kojima se na jednoj strani nalazi  , a na drugoj
, a na drugoj  . Borna ima
. Borna ima  takvih kovanica poredanih u niz slijeva nadesno te započinje proces sljedećih poteza: ako točno
takvih kovanica poredanih u niz slijeva nadesno te započinje proces sljedećih poteza: ako točno 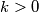 kovanica pokazuje
kovanica pokazuje  ,
,  -tu kovanicu slijeva okreće na drugu stranu; u suprotnom sve kovanice pokazuju
-tu kovanicu slijeva okreće na drugu stranu; u suprotnom sve kovanice pokazuju  i proces staje. Na primjer, ako je
i proces staje. Na primjer, ako je 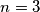 , proces koji započinje konfiguracijom
, proces koji započinje konfiguracijom 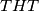 je
je 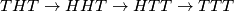 te on staje nakon
te on staje nakon  poteza.
poteza.
(a) Dokaži da, za svaku početnu konfiguraciju, proces staje nakon konačno mnogo poteza.
(b) Za svaku početnu konfiguraciju  , neka je
, neka je 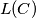 broj poteza potrebnih da proces stane. Na primjer, za
broj poteza potrebnih da proces stane. Na primjer, za 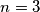 je
je 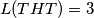 i
i 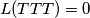 . Odredi aritmetičku sredinu brojeva
. Odredi aritmetičku sredinu brojeva 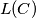 po svih
po svih 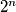 mogućnosti početne konfiguracije
mogućnosti početne konfiguracije  .
.
Izvor: Međunarodna matematička olimpijada 2019, problem 5
 Školjka
Školjka 
