IMO 2019 zadatak 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0Neka je  šiljastokutni trokut takav da je
šiljastokutni trokut takav da je 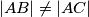 te neka je
te neka je  središte njegove upisane kružnice
središte njegove upisane kružnice  . Kružnica
. Kružnica  dodiruje stranice
dodiruje stranice  ,
,  i
i  u točkama
u točkama  ,
,  i
i  , redom. Pravac kroz točku
, redom. Pravac kroz točku  okomit na pravac
okomit na pravac  siječe kružnicu
siječe kružnicu  ponovno u točki
ponovno u točki  . Pravac
. Pravac 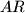 siječe kružnicu
siječe kružnicu  ponovno u točki
ponovno u točki  . Kružnice opisane trokutima
. Kružnice opisane trokutima 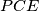 i
i 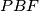 sijeku se ponovno u točki
sijeku se ponovno u točki  .
.
Dokaži da se pravci 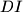 i
i  sijeku na pravcu kroz točku
sijeku na pravcu kroz točku  okomitom na pravac
okomitom na pravac 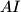 .
.
Izvor: Međunarodna matematička olimpijada 2019, problem 6
 Školjka
Školjka 
