HMO 2022 - Prvi dan - Zadatak 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 5,0Neka je  šiljastokutan trokut u kojem je
šiljastokutan trokut u kojem je 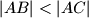 te neka je kružnica
te neka je kružnica  sa središtem
sa središtem  njegova opisana kružnica. Neka su
njegova opisana kružnica. Neka su  i
i  točke redom na stranicama
točke redom na stranicama  i
i  takve da je
takve da je 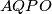 paralelogram. Neka su
paralelogram. Neka su  i
i  sjecišta simetrale dužine
sjecišta simetrale dužine 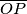 s kružnicom
s kružnicom  , pri čemu je
, pri čemu je  na kraćem luku
na kraćem luku 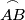 . Neka je
. Neka je  drugo sjecište pravca
drugo sjecište pravca 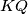 i kružnice
i kružnice  .
.
Dokaži da točka  pripada simetrali kuta
pripada simetrali kuta 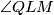 .
.
Izvor: Hrvatska matematička olimpijada 2022.
 Školjka
Školjka 
