Općinsko natjecanje 2002 SŠ3 3
Dodao/la:
arhiva2. travnja 2012. Ako je
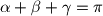
, dokažite sljedeći trigonometrijski identitet
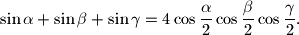
%V0
Ako je $\alpha +\beta +\gamma =\pi $, dokažite sljedeći trigonometrijski identitet $$
\sin \alpha +\sin \beta +\sin \gamma
=4\cos \frac{\alpha }{2}\cos
\frac{\beta }{2}\cos \frac{\gamma }{2}.
$$
Izvor: Općinsko natjecanje iz matematike 2002