Unutar danog trokuta, čije opisana i upisana kružnica imaju središta  i
i  i polumjere
i polumjere  i
i  , nacrtane su četiri jednake kružnice polumjera
, nacrtane su četiri jednake kružnice polumjera  . Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki
. Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki  . Dokažite da točka
. Dokažite da točka  leži na pravcu određenom točkama
leži na pravcu određenom točkama  i
i  . Nađite polumjer
. Nađite polumjer  .
.
 i
i  i polumjere
i polumjere  i
i  , nacrtane su četiri jednake kružnice polumjera
, nacrtane su četiri jednake kružnice polumjera  . Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki
. Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki  . Dokažite da točka
. Dokažite da točka  leži na pravcu određenom točkama
leži na pravcu određenom točkama  i
i  . Nađite polumjer
. Nađite polumjer  .
.  Školjka
Školjka 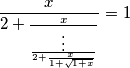 u kojoj ima
u kojoj ima 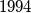 razlomačke crte.
razlomačke crte.  paralelograma
paralelograma  spuštene su okomice
spuštene su okomice 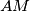 i
i 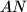 na pravce
na pravce  i
i  . Dokažite da su trokuti
. Dokažite da su trokuti  i
i 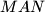 slični.
slični. 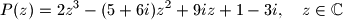 znajući da je bar jedan od njih realan.
znajući da je bar jedan od njih realan. 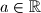 su sva rješenja jednadžbe
su sva rješenja jednadžbe 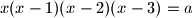 realna?
realna? 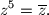
 . Kolika je duljina veće stranice?
. Kolika je duljina veće stranice? 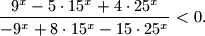
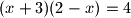 zaključio da je ili
zaključio da je ili 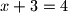 ili
ili 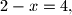 tj. da je
tj. da je  ili
ili 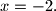 Iako je zaključivanje pogrešno, rješenje je ispravno. Odredite
Iako je zaključivanje pogrešno, rješenje je ispravno. Odredite 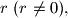 tako da se za dane brojeve
tako da se za dane brojeve  i
i  istim zaključivanjem iz jednadžbe
istim zaključivanjem iz jednadžbe 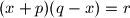 dobije ispravno rješenje.
dobije ispravno rješenje. 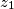 ,
, 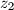 i
i 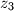 kompleksni brojevi takvi da je
kompleksni brojevi takvi da je 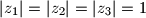 i
i 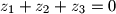 . Dokažite da izraz
. Dokažite da izraz 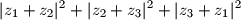 poprima jednu te istu vrijednost za svaki izbor kompleksnih brojeva koji zadovoljavaju gornje uvjete.
poprima jednu te istu vrijednost za svaki izbor kompleksnih brojeva koji zadovoljavaju gornje uvjete.  na kružnicu diraju je u točkama
na kružnicu diraju je u točkama  . Neka je
. Neka je  na kružnici, različita od
na kružnici, različita od 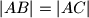 . Dokažite da je
. Dokažite da je 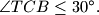
 koordinatne ravnine za koje je
koordinatne ravnine za koje je 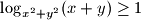 odredite onu koja ima najveću apscisu.
odredite onu koja ima najveću apscisu. 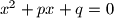 , gdje je
, gdje je 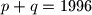 , su cijeli brojevi. Nađite ta rješenja.
, su cijeli brojevi. Nađite ta rješenja. 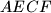 upisani su u istu kružnicu. Izrazite omjer njihovih površina pomoću duljina njihovih stranica.
upisani su u istu kružnicu. Izrazite omjer njihovih površina pomoću duljina njihovih stranica. 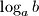 ,
, 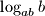 ,
, 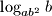 i
i 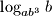 , ako je
, ako je 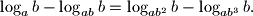
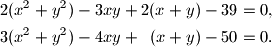
 i
i  tako da za svaki
tako da za svaki ![x \in [-1,1]](/media/m/7/e/8/7e8015685c27a48355d0e72797879b08.png) vrijedi nejednakost
vrijedi nejednakost 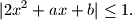
 za koji postoji
za koji postoji  (u dekadskom sustavu) s ovim svojstvima:
(u dekadskom sustavu) s ovim svojstvima:
 ,
, 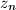 su međusobno različiti brojevi;
su međusobno različiti brojevi; za svaki
za svaki 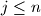 ,
, 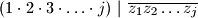 .
. i
i  . Konstruirajte kvadrat tako da mu je jedan vrh u točki
. Konstruirajte kvadrat tako da mu je jedan vrh u točki  za koje je
za koje je 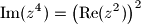 i skicirajte ga u kompleksnoj ravnini.
i skicirajte ga u kompleksnoj ravnini. 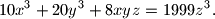
 Odredite sve četveroznamenkaste brojeve koji su jednaki četvrtoj potenciji sume svojih znamenaka.
Odredite sve četveroznamenkaste brojeve koji su jednaki četvrtoj potenciji sume svojih znamenaka. Dokažite da ne postoji peteroznamenkasti broj koji je jednak petoj potenciji sume svojih znamenaka.
Dokažite da ne postoji peteroznamenkasti broj koji je jednak petoj potenciji sume svojih znamenaka. 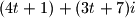 , gdje je
, gdje je  realan broj. Što je taj skup?
realan broj. Što je taj skup?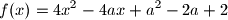 na intervalu
na intervalu ![[0,2]](/media/m/6/8/f/68fca448efcc3c5617dbc68ff5789a46.png) jednaka
jednaka  ?
? 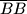 i
i 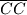 . Kroz ortocentar
. Kroz ortocentar  je povučen pravac koji siječe stranice trokuta
je povučen pravac koji siječe stranice trokuta  i
i  redom u točkama
redom u točkama 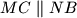 .
. 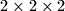 , te se prebroji koliko točaka ima na svakoj strani. Može li se na taj način dobiti šest uzastopnih prirodnih brojeva?
, te se prebroji koliko točaka ima na svakoj strani. Može li se na taj način dobiti šest uzastopnih prirodnih brojeva? 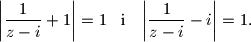
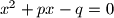 i gdje je
i gdje je 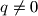 , oba rješenja cjelobrojna, dokažite da tada postoje prirodni brojevi
, oba rješenja cjelobrojna, dokažite da tada postoje prirodni brojevi 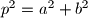 .
.