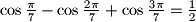Međunarodna matematička olimpijada
[ IMO ]
An arbitrary point  is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 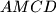 and
and 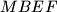 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments  and
and 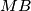 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 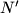 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 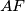 and
and  .
.
a) Prove that and
and 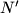 coincide;
coincide;
b) Prove that the straight lines pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
;
c) Find the locus of the midpoints of the segments as
as  varies between
varies between  and
and  .
.
 is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 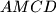 and
and 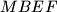 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments  and
and 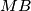 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 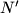 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 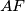 and
and  .
. a) Prove that
 and
and 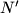 coincide;
coincide; b) Prove that the straight lines
 pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
; c) Find the locus of the midpoints of the segments
 as
as  varies between
varies between  and
and  .
. Consider a cone of revolution with an inscribed sphere tangent to the base of the cone. A cylinder is circumscribed about this sphere so that one of its bases lies in the base of the cone. let 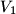 be the volume of the cone and
be the volume of the cone and 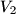 be the volume of the cylinder.
be the volume of the cylinder.
a) Prove that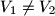 ;
;
b) Find the smallest number for which
for which 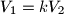 ; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
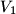 be the volume of the cone and
be the volume of the cone and 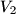 be the volume of the cylinder.
be the volume of the cylinder. a) Prove that
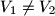 ;
; b) Find the smallest number
 for which
for which 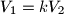 ; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone. An isosceles trapezoid with bases  and
and  and altitude
and altitude  is given.
is given.
a) On the axis of symmetry of this trapezoid, find all points such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
;
b) Calculate the distance of from either base;
from either base;
c) Determine under what conditions such points actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise.
 and
and  and altitude
and altitude  is given.
is given. a) On the axis of symmetry of this trapezoid, find all points
 such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
; b) Calculate the distance of
 from either base;
from either base; c) Determine under what conditions such points
 actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise. Consider a plane  and three non-collinear points
and three non-collinear points  on the same side of
on the same side of  ; suppose the plane determined by these three points is not parallel to
; suppose the plane determined by these three points is not parallel to  . In plane
. In plane  take three arbitrary points
take three arbitrary points 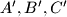 . Let
. Let 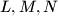 be the midpoints of segments
be the midpoints of segments 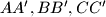 ; Let
; Let  be the centroid of the triangle
be the centroid of the triangle 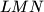 . (We will not consider positions of the points
. (We will not consider positions of the points 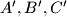 such that the points
such that the points 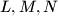 do not form a triangle.) What is the locus of point
do not form a triangle.) What is the locus of point  as
as 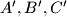 range independently over the plane
range independently over the plane  ?
?
 and three non-collinear points
and three non-collinear points  on the same side of
on the same side of  ; suppose the plane determined by these three points is not parallel to
; suppose the plane determined by these three points is not parallel to  . In plane
. In plane  take three arbitrary points
take three arbitrary points 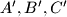 . Let
. Let 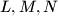 be the midpoints of segments
be the midpoints of segments 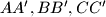 ; Let
; Let  be the centroid of the triangle
be the centroid of the triangle 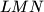 . (We will not consider positions of the points
. (We will not consider positions of the points 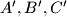 such that the points
such that the points 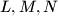 do not form a triangle.) What is the locus of point
do not form a triangle.) What is the locus of point  as
as 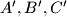 range independently over the plane
range independently over the plane  ?
? Consider the cube 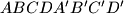 (
( and
and 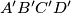 are the upper and lower bases, repsectively, and edges
are the upper and lower bases, repsectively, and edges 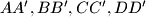 are parallel). The point
are parallel). The point  moves at a constant speed along the perimeter of the square
moves at a constant speed along the perimeter of the square  in the direction
in the direction 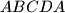 , and the point
, and the point  moves at the same rate along the perimiter of the square
moves at the same rate along the perimiter of the square 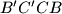 in the direction
in the direction 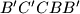 . Points
. Points  and
and  begin their motion at the same instant from the starting positions
begin their motion at the same instant from the starting positions  and
and 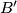 , respectively. Determine and draw the locus of the midpionts of the segments
, respectively. Determine and draw the locus of the midpionts of the segments  .
.
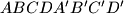 (
( and
and 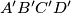 are the upper and lower bases, repsectively, and edges
are the upper and lower bases, repsectively, and edges 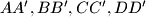 are parallel). The point
are parallel). The point  moves at a constant speed along the perimeter of the square
moves at a constant speed along the perimeter of the square  in the direction
in the direction 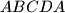 , and the point
, and the point  moves at the same rate along the perimiter of the square
moves at the same rate along the perimiter of the square 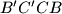 in the direction
in the direction 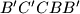 . Points
. Points  and
and  begin their motion at the same instant from the starting positions
begin their motion at the same instant from the starting positions  and
and 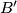 , respectively. Determine and draw the locus of the midpionts of the segments
, respectively. Determine and draw the locus of the midpionts of the segments  .
.  Školjka
Školjka 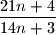 is irreducible for every natural number
is irreducible for every natural number  .
.  is
is 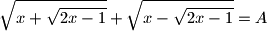 given
given 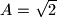 ;
; 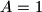 ;
; 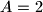 ,
,  be real numbers. Consider the quadratic equation in
be real numbers. Consider the quadratic equation in 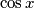
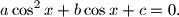 Using the numbers
Using the numbers 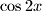 whose roots are the same as those of the original equation. Compare the equation in
whose roots are the same as those of the original equation. Compare the equation in 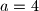 ,
,  ,
, 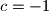 .
.  in the plane
in the plane 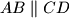 ) in which a circle can be inscribed, and with vertices
) in which a circle can be inscribed, and with vertices  lying in planes
lying in planes 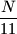 is equal to the sum of the squares of the digits of
is equal to the sum of the squares of the digits of 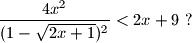
 , given
, given  ,
,  (the altitudes from
(the altitudes from 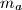 , the median from vertex
, the median from vertex  and
and 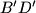 ;
;  which lie on the segment
which lie on the segment 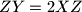 .
. 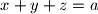
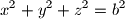
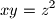 where
where  are constants. Give the conditions that
are constants. Give the conditions that 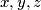 are distinct positive numbers.
are distinct positive numbers. 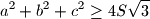
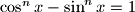 where
where 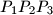 and a point
and a point 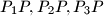 intersect the opposite sides in points
intersect the opposite sides in points 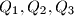 respectively. Prove that, of the numbers
respectively. Prove that, of the numbers 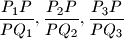
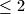 and at least one is
and at least one is 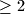
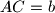 ,
, 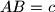 and
and 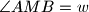 , where
, where 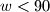 . Prove that a solution exists if and only if
. Prove that a solution exists if and only if 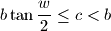 In what case does the equality hold?
In what case does the equality hold? 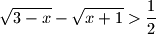
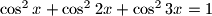
 there are given three distinct points
there are given three distinct points  be the radius of its circumscribed circle and
be the radius of its circumscribed circle and  be the radius of its inscribed circle. Prove that the distance
be the radius of its inscribed circle. Prove that the distance  between the centers of these two circle is
between the centers of these two circle is 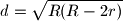
 has the following property: there exist five spheres, each tangent to the edges
has the following property: there exist five spheres, each tangent to the edges 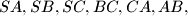 or to their extensions.
or to their extensions. 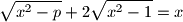 where
where  , all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation
, all of whose interior angles are equal, the lengths of consecutive sides satisfy the relation 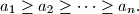
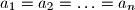 .
.  of the system
of the system 



 where
where  is a parameter.
is a parameter.