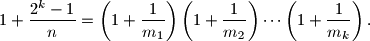In the plane,  red points and
red points and  blue points are marked so that no three of the marked points are collinear. One needs to draw
blue points are marked so that no three of the marked points are collinear. One needs to draw  lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors.
lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors.
Find the minimal value of such that the goal is attainable for every possible configuration of
such that the goal is attainable for every possible configuration of  points.
points.
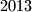 red points and
red points and 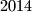 blue points are marked so that no three of the marked points are collinear. One needs to draw
blue points are marked so that no three of the marked points are collinear. One needs to draw  lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors.
lines not passing through the marked points and dividing the plane into several regions. The goal is to do it in such a way that no region contains points of both colors. Find the minimal value of
 such that the goal is attainable for every possible configuration of
such that the goal is attainable for every possible configuration of 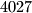 points.
points. Let  be an integer. Consider all circular arrangements of the numbers
be an integer. Consider all circular arrangements of the numbers 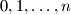 ; the
; the  rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers
rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers 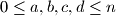 with
with 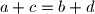 , the chord joining numbers
, the chord joining numbers  and
and  does not intersect the chord joining numbers
does not intersect the chord joining numbers  and
and  .
.
Let be the number of beautiful arrangements of
be the number of beautiful arrangements of 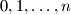 . Let
. Let  be the number of pairs
be the number of pairs 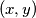 of positive integers such that
of positive integers such that 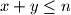 and
and 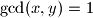 . Prove that
. Prove that 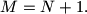
 be an integer. Consider all circular arrangements of the numbers
be an integer. Consider all circular arrangements of the numbers 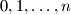 ; the
; the  rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers
rotations of an arrangement are considered to be equal. A circular arrangement is called beautiful if, for any four distinct numbers 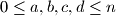 with
with 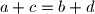 , the chord joining numbers
, the chord joining numbers  and
and  does not intersect the chord joining numbers
does not intersect the chord joining numbers  and
and  .
.Let
 be the number of beautiful arrangements of
be the number of beautiful arrangements of 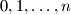 . Let
. Let  be the number of pairs
be the number of pairs 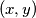 of positive integers such that
of positive integers such that 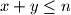 and
and 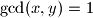 . Prove that
. Prove that 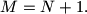
Let  be an acute-angled triangle with orthocenter
be an acute-angled triangle with orthocenter  , and let
, and let  be a point on side
be a point on side  . Denote by
. Denote by  and
and  the feet of the altitudes from
the feet of the altitudes from  and
and  , respectively. Denote by
, respectively. Denote by 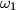 the circumcircle of
the circumcircle of 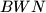 , and let
, and let  be the point on
be the point on 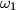 which is diametrically opposite to
which is diametrically opposite to  . Analogously, denote by
. Analogously, denote by 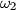 the circumcircle of
the circumcircle of 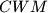 , and let
, and let  be the point on
be the point on 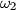 which is diametrically opposite to
which is diametrically opposite to  . Prove that
. Prove that  ,
,  and
and  are collinear.
are collinear.
 be an acute-angled triangle with orthocenter
be an acute-angled triangle with orthocenter  , and let
, and let  be a point on side
be a point on side  . Denote by
. Denote by  and
and  the feet of the altitudes from
the feet of the altitudes from  and
and  , respectively. Denote by
, respectively. Denote by 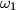 the circumcircle of
the circumcircle of 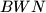 , and let
, and let  be the point on
be the point on 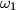 which is diametrically opposite to
which is diametrically opposite to  . Analogously, denote by
. Analogously, denote by 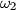 the circumcircle of
the circumcircle of 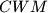 , and let
, and let  be the point on
be the point on 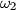 which is diametrically opposite to
which is diametrically opposite to  . Prove that
. Prove that  ,
,  and
and  are collinear.
are collinear.  Školjka
Školjka  be the set of positive rational numbers. Let
be the set of positive rational numbers. Let 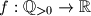 be a function satisfying the conditions
be a function satisfying the conditions 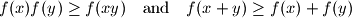 for all
for all 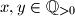 . Given that
. Given that 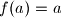 for some rational
for some rational 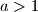 , prove that
, prove that 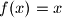 for all
for all 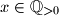 .
.  touch its side
touch its side  . Define the points
. Define the points  and
and  analogously. Suppose that the circumcentre of the triangle
analogously. Suppose that the circumcentre of the triangle 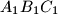 lies on the circumcircle of the triangle
lies on the circumcircle of the triangle  there exist
there exist 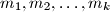 such that
such that