Twenty-one girls and twenty-one boys took part in a mathematical competition. It turned out that each contestant solved at most six problems, and for each pair of a girl and a boy, there was at least one problem that was solved by both the girl and the boy. Show that there is a problem that was solved by at least three girls and at least three boys.
 Školjka
Školjka  ,
, 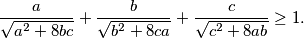
 be an odd integer greater than 1 and let
be an odd integer greater than 1 and let 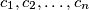 be integers. For each permutation
be integers. For each permutation 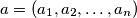 of
of 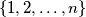 , define
, define 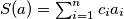 . Prove that there exist permutations
. Prove that there exist permutations 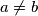 of
of 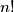 is a divisor of
is a divisor of 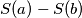 .
.  . Let
. Let  be the foot of the altitude of triangle
be the foot of the altitude of triangle  , and let
, and let  be the circumcenter of triangle
be the circumcenter of triangle 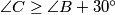 . Prove that
. Prove that 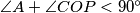 .
. 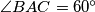 . Let
. Let 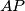 bisect
bisect 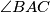 and let
and let 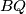 bisect
bisect 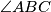 , with
, with  and
and  on
on  . If
. If 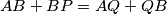 , what are the angles of the triangle?
, what are the angles of the triangle?  be positive integers and suppose that
be positive integers and suppose that  Prove that
Prove that  is not prime.
is not prime.