A set  of points from the space will be called completely symmetric if it has at least three elements and fulfills the condition that for every two distinct points
of points from the space will be called completely symmetric if it has at least three elements and fulfills the condition that for every two distinct points  and
and  from
from  , the perpendicular bisector plane of the segment
, the perpendicular bisector plane of the segment  is a plane of symmetry for
is a plane of symmetry for  . Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, or a regular tetrahedron or a regular octahedron.
. Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, or a regular tetrahedron or a regular octahedron.
 of points from the space will be called completely symmetric if it has at least three elements and fulfills the condition that for every two distinct points
of points from the space will be called completely symmetric if it has at least three elements and fulfills the condition that for every two distinct points  and
and  from
from  , the perpendicular bisector plane of the segment
, the perpendicular bisector plane of the segment  is a plane of symmetry for
is a plane of symmetry for  . Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, or a regular tetrahedron or a regular octahedron.
. Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, or a regular tetrahedron or a regular octahedron.  Školjka
Školjka  be a fixed integer. Find the least constant
be a fixed integer. Find the least constant  such the inequality
such the inequality 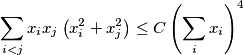
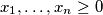 (the sum on the left consists of
(the sum on the left consists of 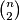 summands). For this constant
summands). For this constant 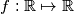 such that
such that 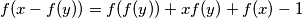
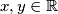 .
.  be an even positive integer. We say that two different cells of a
be an even positive integer. We say that two different cells of a 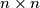 board are neighboring if they have a common side. Find the minimal number of cells on he
board are neighboring if they have a common side. Find the minimal number of cells on he 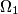 and
and 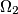 touch internally the circle
touch internally the circle  in M and N and the center of
in M and N and the center of 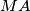 and
and 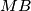 intersects
intersects  . Prove that
. Prove that  .
. 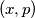 such that p is a prime,
such that p is a prime, 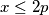 and
and 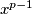 is a divisor of
is a divisor of 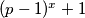 .
.