Let 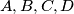 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 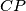 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 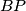 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 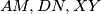 are concurrent.
are concurrent.
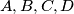 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 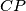 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 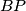 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 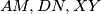 are concurrent.
are concurrent.  Školjka
Školjka  ,
,  ,
,  be positive real numbers such that
be positive real numbers such that 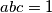 . Prove that
. Prove that 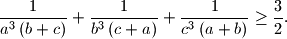
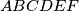 be a convex hexagon with
be a convex hexagon with 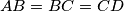 and
and 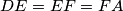 , such that
, such that 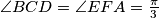 . Suppose
. Suppose  and
and  are points in the interior of the hexagon such that
are points in the interior of the hexagon such that 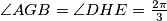 . Prove that
. Prove that 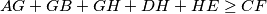 .
. 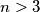 for which there exist
for which there exist  points
points 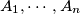 in the plane, no three collinear, and real numbers
in the plane, no three collinear, and real numbers 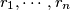 such that for
such that for 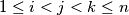 , the area of
, the area of 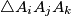 is
is 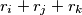 .
. 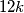 people, each person exchanges greetings with exactly
people, each person exchanges greetings with exactly 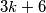 others. For any two people, the number who exchange greetings with both is the same. How many people are at the meeting?
others. For any two people, the number who exchange greetings with both is the same. How many people are at the meeting? 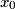 for which there exists a sequence
for which there exists a sequence 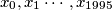 of positive reals with
of positive reals with 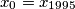 , such that
, such that 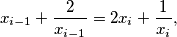
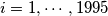 .
.