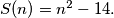Consider 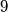 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
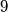 points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of
points in space, no four of which are coplanar. Each pair of points is joined by an edge (that is, a line segment) and each edge is either colored blue or red or left uncolored. Find the smallest value of  such that whenever exactly
such that whenever exactly  edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color.
edges are colored, the set of colored edges necessarily contains a triangle all of whose edges have the same color. Let 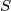 be a finite set of points in three-dimensional space. Let
be a finite set of points in three-dimensional space. Let 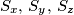 be the sets consisting of the orthogonal projections of the points of
be the sets consisting of the orthogonal projections of the points of 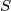 onto the
onto the 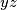 -plane,
-plane,  -plane,
-plane, 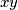 -plane, respectively. Prove that
-plane, respectively. Prove that 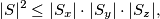 where
where 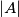 denotes the number of elements in the finite set
denotes the number of elements in the finite set  .
.
Note Note: The orthogonal projection of a point onto a plane is the foot of the perpendicular from that point to the plane.
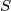 be a finite set of points in three-dimensional space. Let
be a finite set of points in three-dimensional space. Let 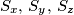 be the sets consisting of the orthogonal projections of the points of
be the sets consisting of the orthogonal projections of the points of 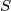 onto the
onto the 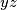 -plane,
-plane,  -plane,
-plane, 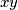 -plane, respectively. Prove that
-plane, respectively. Prove that 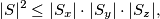 where
where 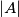 denotes the number of elements in the finite set
denotes the number of elements in the finite set  .
. Note Note: The orthogonal projection of a point onto a plane is the foot of the perpendicular from that point to the plane.
 Školjka
Školjka 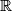 denote the set of all real numbers. Find all functions
denote the set of all real numbers. Find all functions 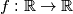 such that
such that 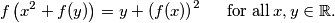
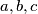 with
with 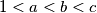 such that
such that 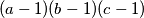 is a divisor of
is a divisor of 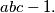
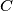 be a circle,
be a circle, 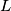 a line tangent to the circle
a line tangent to the circle 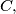 and
and 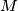 a point on
a point on 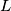 . Find the locus of all points
. Find the locus of all points 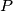 with the following property: there exists two points
with the following property: there exists two points 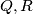 on
on 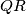 and
and 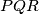 .
. 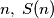 is defined to be the greatest integer such that, for every positive integer
is defined to be the greatest integer such that, for every positive integer 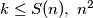 can be written as the sum of
can be written as the sum of 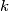 positive squares.
positive squares. 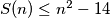 for each
for each 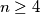 .
. 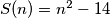 .
.