Let  and consider a set
and consider a set  of
of 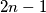 distinct points on a circle. Suppose that exactly
distinct points on a circle. Suppose that exactly  of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly
of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly  points from
points from  . Find the smallest value of
. Find the smallest value of  so that every such coloring of
so that every such coloring of  points of
points of  is good.
is good.
 and consider a set
and consider a set  of
of 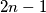 distinct points on a circle. Suppose that exactly
distinct points on a circle. Suppose that exactly  of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly
of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly  points from
points from  . Find the smallest value of
. Find the smallest value of  so that every such coloring of
so that every such coloring of  points of
points of  is good.
is good. Given an initial integer 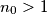 , two players,
, two players,  and
and  , choose integers
, choose integers 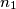 ,
, 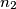 ,
, 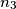 ,
,  alternately according to the following rules :
alternately according to the following rules :
I.) Knowing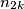 ,
,  chooses any integer
chooses any integer 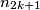 such that
such that
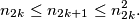
II.) Knowing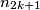 ,
,  chooses any integer
chooses any integer 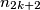 such that
such that
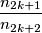
is a prime raised to a positive integer power.
Player wins the game by choosing the number 1990; player
wins the game by choosing the number 1990; player  wins by choosing the number 1. For which
wins by choosing the number 1. For which 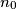 does :
does :
a.) have a winning strategy?
have a winning strategy?
b.) have a winning strategy?
have a winning strategy?
c.) Neither player have a winning strategy?
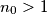 , two players,
, two players,  and
and  , choose integers
, choose integers 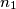 ,
, 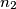 ,
, 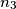 ,
,  alternately according to the following rules :
alternately according to the following rules : I.) Knowing
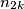 ,
,  chooses any integer
chooses any integer 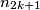 such that
such that 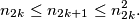
II.) Knowing
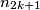 ,
,  chooses any integer
chooses any integer 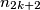 such that
such that 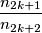
is a prime raised to a positive integer power.
Player
 wins the game by choosing the number 1990; player
wins the game by choosing the number 1990; player  wins by choosing the number 1. For which
wins by choosing the number 1. For which 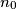 does :
does : a.)
 have a winning strategy?
have a winning strategy? b.)
 have a winning strategy?
have a winning strategy? c.) Neither player have a winning strategy?
 Školjka
Školjka  and
and  of a circle intersect at a point
of a circle intersect at a point  be an interior point of the segment
be an interior point of the segment 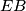 . The tangent line at
. The tangent line at  ,
,  and
and  at
at  and
and  , respectively. If
, respectively. If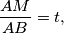
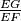 in terms of
in terms of  .
. 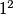 ,
, 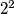 ,
, 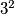 ,
,  ,
, 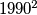 in some order.
in some order. 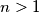 such that
such that 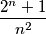
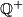 be the set of positive rational numbers. Construct a function
be the set of positive rational numbers. Construct a function 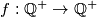 such that
such that 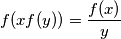
 ,
,  in
in