Given a finite set of points in the plane, each with integer coordinates, is it always possible to color the points red or white so that for any straight line  parallel to one of the coordinate axes the difference (in absolute value) between the numbers of white and red points on
parallel to one of the coordinate axes the difference (in absolute value) between the numbers of white and red points on  is not greater than
is not greater than  ?
?
 parallel to one of the coordinate axes the difference (in absolute value) between the numbers of white and red points on
parallel to one of the coordinate axes the difference (in absolute value) between the numbers of white and red points on  is not greater than
is not greater than  ?
? To each vertex of a regular pentagon an integer is assigned, so that the sum of all five numbers is positive. If three consecutive vertices are assigned the numbers 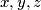 respectively, and
respectively, and 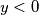 , then the following operation is allowed:
, then the following operation is allowed: 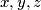 are replaced by
are replaced by 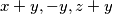 respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.
respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.
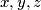 respectively, and
respectively, and 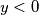 , then the following operation is allowed:
, then the following operation is allowed: 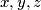 are replaced by
are replaced by 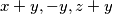 respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.
respectively. Such an operation is performed repeatedly as long as at least one of the five numbers is negative. Determine whether this procedure necessarily comes to an end after a finite number of steps.  Školjka
Školjka  be any positive integer not equal to
be any positive integer not equal to 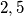 or
or 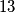 . Show that one can find distinct
. Show that one can find distinct 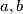 in the set
in the set 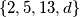 such that
such that 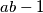 is not a perfect square.
is not a perfect square. 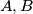 be adjacent vertices of a regular
be adjacent vertices of a regular  -gon (
-gon (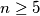 ) with center
) with center  . A triangle
. A triangle 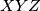 , which is congruent to and initially coincides with
, which is congruent to and initially coincides with 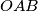 , moves in the plane in such a way that
, moves in the plane in such a way that  and
and  each trace out the whole boundary of the polygon, with
each trace out the whole boundary of the polygon, with  remaining inside the polygon. Find the locus of
remaining inside the polygon. Find the locus of 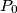 in the plane of the triangle
in the plane of the triangle 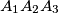 . Define
. Define 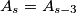 for all
for all 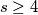 . Construct a set of points
. Construct a set of points 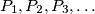 such that
such that 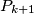 is the image of
is the image of 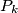 under a rotation center
under a rotation center 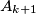 through an angle
through an angle 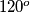 clockwise for
clockwise for 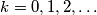 . Prove that if
. Prove that if 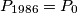 , then the triangle
, then the triangle