Let  be a square with sides length
be a square with sides length 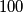 . Let
. Let  be a path within
be a path within  which does not meet itself and which is composed of line segments
which does not meet itself and which is composed of line segments 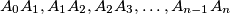 with
with 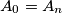 . Suppose that for every point
. Suppose that for every point  on the boundary of
on the boundary of  there is a point of
there is a point of  at a distance from
at a distance from  no greater than
no greater than  . Prove that there are two points
. Prove that there are two points  and
and  of
of  such that the distance between
such that the distance between  and
and  is not greater than
is not greater than  and the length of the part of
and the length of the part of  which lies between
which lies between  and
and  is not smaller than
is not smaller than 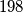 .
.
 be a square with sides length
be a square with sides length 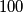 . Let
. Let  be a path within
be a path within  which does not meet itself and which is composed of line segments
which does not meet itself and which is composed of line segments 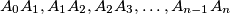 with
with 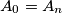 . Suppose that for every point
. Suppose that for every point  on the boundary of
on the boundary of  there is a point of
there is a point of  at a distance from
at a distance from  no greater than
no greater than  . Prove that there are two points
. Prove that there are two points  and
and  of
of  such that the distance between
such that the distance between  and
and  is not greater than
is not greater than  and the length of the part of
and the length of the part of  which lies between
which lies between  and
and  is not smaller than
is not smaller than 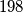 .
. A non-isosceles triangle 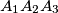 has sides
has sides 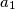 ,
, 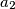 ,
, 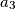 with the side
with the side 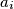 lying opposite to the vertex
lying opposite to the vertex 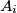 . Let
. Let 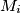 be the midpoint of the side
be the midpoint of the side 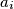 , and let
, and let 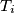 be the point where the inscribed circle of triangle
be the point where the inscribed circle of triangle 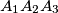 touches the side
touches the side 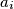 . Denote by
. Denote by 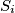 the reflection of the point
the reflection of the point 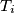 in the interior angle bisector of the angle
in the interior angle bisector of the angle 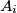 . Prove that the lines
. Prove that the lines 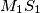 ,
, 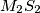 and
and 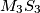 are concurrent.
are concurrent.
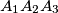 has sides
has sides 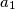 ,
, 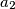 ,
, 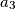 with the side
with the side 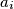 lying opposite to the vertex
lying opposite to the vertex 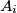 . Let
. Let 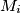 be the midpoint of the side
be the midpoint of the side 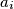 , and let
, and let 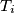 be the point where the inscribed circle of triangle
be the point where the inscribed circle of triangle 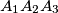 touches the side
touches the side 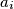 . Denote by
. Denote by 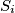 the reflection of the point
the reflection of the point 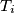 in the interior angle bisector of the angle
in the interior angle bisector of the angle 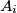 . Prove that the lines
. Prove that the lines 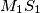 ,
, 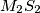 and
and 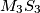 are concurrent.
are concurrent.  Školjka
Školjka  is defined on the positive integers and takes non-negative integer values.
is defined on the positive integers and takes non-negative integer values. 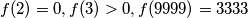 and for all
and for all 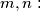
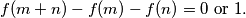 Determine
Determine 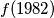 .
. 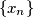 of positive reals such that
of positive reals such that 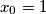 and
and 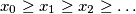 .
.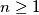 such that:
such that: 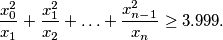
 :
: 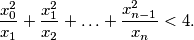
 and
and 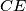 of the regular hexagon
of the regular hexagon 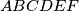 are divided by inner points
are divided by inner points  and
and  respectively, so that
respectively, so that 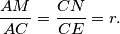 Determine
Determine  if
if  and
and 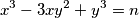 has a solution in integers
has a solution in integers 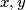 , then it has at least three such solutions. Show that the equation has no solutions in integers for
, then it has at least three such solutions. Show that the equation has no solutions in integers for 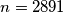 .
.