We consider a prism which has the upper and inferior basis the pentagons: 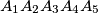 and
and 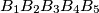 . Each of the sides of the two pentagons and the segments
. Each of the sides of the two pentagons and the segments 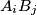 with
with 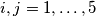 is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
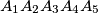 and
and 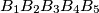 . Each of the sides of the two pentagons and the segments
. Each of the sides of the two pentagons and the segments 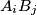 with
with 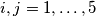 is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color. Two circles in a plane intersect.  is one of the points of intersection. Starting simultaneously from
is one of the points of intersection. Starting simultaneously from  two points move with constant speed, each travelling along its own circle in the same sense. The two points return to
two points move with constant speed, each travelling along its own circle in the same sense. The two points return to  simultaneously after one revolution. Prove that there is a fixed point
simultaneously after one revolution. Prove that there is a fixed point  in the plane such that the two points are always equidistant from
in the plane such that the two points are always equidistant from 
 is one of the points of intersection. Starting simultaneously from
is one of the points of intersection. Starting simultaneously from  two points move with constant speed, each travelling along its own circle in the same sense. The two points return to
two points move with constant speed, each travelling along its own circle in the same sense. The two points return to  simultaneously after one revolution. Prove that there is a fixed point
simultaneously after one revolution. Prove that there is a fixed point  in the plane such that the two points are always equidistant from
in the plane such that the two points are always equidistant from 
 Školjka
Školjka  and
and  are natural numbers so that
are natural numbers so that 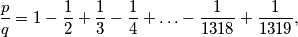 prove that
prove that 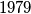 .
.  be opposite vertices of an octagon. A frog starts at vertex
be opposite vertices of an octagon. A frog starts at vertex 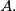 From any vertex except
From any vertex except  be the number of distinct paths of exactly
be the number of distinct paths of exactly  jumps ending at
jumps ending at 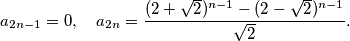
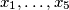 which satisfy the relations
which satisfy the relations 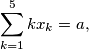
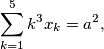
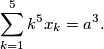
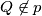 . Determine all the points
. Determine all the points  from
from 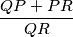 is maximum.
is maximum.