A soldier needs to check if there are any mines in the interior or on the sides of an equilateral triangle  His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?
His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?
 His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?
His detector can detect a mine at a maximum distance equal to half the height of the triangle. The soldier leaves from one of the vertices of the triangle. Which is the minimum distance that he needs to traverse so that at the end of it he is sure that he completed successfully his mission?  is a set of non-constant functions
is a set of non-constant functions  . Each
. Each  is defined on the real line and has the form
is defined on the real line and has the form 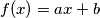 for some real
for some real 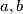 . If
. If  and
and  are in
are in  , then so is
, then so is 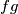 , where
, where 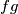 is defined by
is defined by 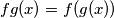 . If
. If  is in
is in  , then so is the inverse
, then so is the inverse 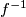 . If
. If 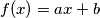 , then
, then 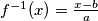 . Every
. Every  in
in  has a fixed point (in other words we can find
has a fixed point (in other words we can find 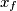 such that
such that 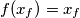 . Prove that all the functions in
. Prove that all the functions in  have a common fixed point.
have a common fixed point.  Školjka
Školjka  and all situated in the same semi-plane determined by a straight line which goes through
and all situated in the same semi-plane determined by a straight line which goes through  is at least 1.
is at least 1.  of points in space, not all situated in the same plane, so that for any straight line
of points in space, not all situated in the same plane, so that for any straight line  which contains at least two points from M there exists another straight line
which contains at least two points from M there exists another straight line 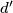 , parallel with
, parallel with 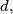 but distinct from
but distinct from 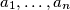 be
be  positive numbers and
positive numbers and 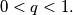 Determine
Determine 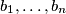 so that:
so that: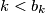 for all
for all 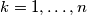 ,
,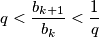 for all
for all 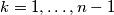 ,
,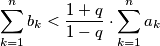 .
. 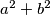 when
when 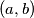 traverses all the pairs of real numbers for which the equation
traverses all the pairs of real numbers for which the equation 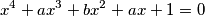 has at least one real root.
has at least one real root.