In tetrahedron

, vertex

is connected with
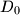
, the centrod if

. Line parallel to
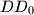
are drawn through
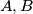
and

. These lines intersect the planes
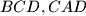
and
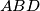
in points
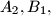
and

, respectively. Prove that the volume of

is one third the volume of
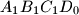
. Is the result if point
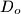
is selected anywhere within

?
%V0
In tetrahedron $ABCD$, vertex $D$ is connected with $D_0$, the centrod if $\triangle ABC$. Line parallel to $DD_0$ are drawn through $A,B$ and $C$. These lines intersect the planes $BCD, CAD$ and $ABD$ in points $A_2, B_1,$ and $C_1$, respectively. Prove that the volume of $ABCD$ is one third the volume of $A_1B_1C_1D_0$. Is the result if point $D_o$ is selected anywhere within $\triangle ABC$?
 Školjka
Školjka  with sides
with sides  . Tangents to the circle parallel to the sides of the triangle are contructe. Each of these tangents cuts off a triagnle from
. Tangents to the circle parallel to the sides of the triangle are contructe. Each of these tangents cuts off a triagnle from  . In each of these triangles, a circle is inscribed. Find the sum of the areas of all four inscribed circles (in terms of
. In each of these triangles, a circle is inscribed. Find the sum of the areas of all four inscribed circles (in terms of  , vertex
, vertex  is connected with
is connected with 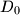 , the centrod if
, the centrod if 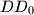 are drawn through
are drawn through 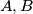 and
and  . These lines intersect the planes
. These lines intersect the planes 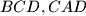 and
and 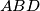 in points
in points 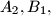 and
and  , respectively. Prove that the volume of
, respectively. Prove that the volume of 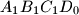 . Is the result if point
. Is the result if point 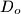 is selected anywhere within
is selected anywhere within