An arbitrary point  is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 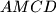 and
and 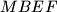 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments  and
and 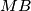 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 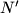 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 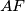 and
and  .
.
a) Prove that and
and 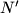 coincide;
coincide;
b) Prove that the straight lines pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
;
c) Find the locus of the midpoints of the segments as
as  varies between
varies between  and
and  .
.
 is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 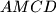 and
and 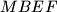 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments  and
and 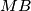 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 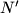 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 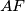 and
and  .
. a) Prove that
 and
and 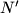 coincide;
coincide; b) Prove that the straight lines
 pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
; c) Find the locus of the midpoints of the segments
 as
as  varies between
varies between  and
and  .
.  Školjka
Školjka 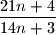 is irreducible for every natural number
is irreducible for every natural number  .
.  is
is 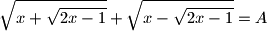 given
given 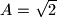 ;
; 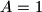 ;
; 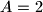 ,
,  be real numbers. Consider the quadratic equation in
be real numbers. Consider the quadratic equation in 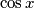
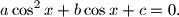 Using the numbers
Using the numbers 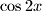 whose roots are the same as those of the original equation. Compare the equation in
whose roots are the same as those of the original equation. Compare the equation in 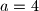 ,
,  ,
, 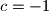 .
.  such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.
such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.  . The point
. The point  in the plane
in the plane  (with
(with 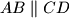 ) in which a circle can be inscribed, and with vertices
) in which a circle can be inscribed, and with vertices  lying in planes
lying in planes