Neka je  prirodni broj. Na ploču koja se sastoji od
prirodni broj. Na ploču koja se sastoji od 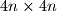 kvadrata postavljeno je točno
kvadrata postavljeno je točno 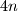 žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.
žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.
Odredi najmanji broj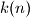 takav da to možemo postići u najviše
takav da to možemo postići u najviše 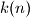 koraka za bilo koji početni raspored.
koraka za bilo koji početni raspored.
 prirodni broj. Na ploču koja se sastoji od
prirodni broj. Na ploču koja se sastoji od 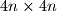 kvadrata postavljeno je točno
kvadrata postavljeno je točno 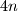 žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.
žetona tako da se u svakom retku i svakom stupcu nalazi točno jedan žeton. U jednom koraku, jedan žeton pomičemo horizontalno ili vertikalno na susjedni kvadrat. Više žetona se u nekom trenutku može nalaziti na istom kvadratu. Žetone trebamo pomaknuti tako da zauzimaju sve kvadrate jedne od dviju dijagonala.Odredi najmanji broj
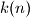 takav da to možemo postići u najviše
takav da to možemo postići u najviše 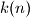 koraka za bilo koji početni raspored.
koraka za bilo koji početni raspored. Na sjevernoj strani ulice nalazi se  kuća. Od zapada prema istoku, kuće su označene brojevima od
kuća. Od zapada prema istoku, kuće su označene brojevima od  do
do  . Svaka kuća ima istaknutu ploču s kućnim brojem. Jednog dana stanovnici te ulice odlučili su našaliti se s poštarom tako da su izmiješali ploče s kućnim brojevima na sljedeći način: svakim dvjema susjednim kućama su točno jednom međusobno zamijenjene ploče koje su u tom trenutku imale.
. Svaka kuća ima istaknutu ploču s kućnim brojem. Jednog dana stanovnici te ulice odlučili su našaliti se s poštarom tako da su izmiješali ploče s kućnim brojevima na sljedeći način: svakim dvjema susjednim kućama su točno jednom međusobno zamijenjene ploče koje su u tom trenutku imale.
Koliko različitih nizova ploča s brojevima se moglo postići na kraju toga dana?
 kuća. Od zapada prema istoku, kuće su označene brojevima od
kuća. Od zapada prema istoku, kuće su označene brojevima od  do
do  . Svaka kuća ima istaknutu ploču s kućnim brojem. Jednog dana stanovnici te ulice odlučili su našaliti se s poštarom tako da su izmiješali ploče s kućnim brojevima na sljedeći način: svakim dvjema susjednim kućama su točno jednom međusobno zamijenjene ploče koje su u tom trenutku imale.
. Svaka kuća ima istaknutu ploču s kućnim brojem. Jednog dana stanovnici te ulice odlučili su našaliti se s poštarom tako da su izmiješali ploče s kućnim brojevima na sljedeći način: svakim dvjema susjednim kućama su točno jednom međusobno zamijenjene ploče koje su u tom trenutku imale.Koliko različitih nizova ploča s brojevima se moglo postići na kraju toga dana?
Promotrite konačno mnogo točaka u ravnini takvih da nikoje tri točke ne leže na jednom pravcu. Svaku od tih točaka možemo obojati crvenom ili zelenom bojom tako da svaki trokut kojem su vrhovi iste boje u svojoj unutrašnjosti sadrži barem jednu točku druge boje.
Koji je najveći mogući broj takvih točaka?
Koji je najveći mogući broj takvih točaka?
Neka je točka  unutar šiljastokutnog trokuta
unutar šiljastokutnog trokuta  takva da je pravac
takva da je pravac  zajednička tangenta kružnica opisanih trokutima
zajednička tangenta kružnica opisanih trokutima 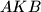 i
i 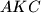 . Neka je točka
. Neka je točka  sjecište pravaca
sjecište pravaca 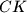 i
i  te neka je točka
te neka je točka  sjecište pravaca
sjecište pravaca 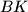 i
i  . Neka je točka
. Neka je točka  sjecište pravca
sjecište pravca  i simetrale dužine
i simetrale dužine 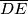 . Opisana kružnica trokuta
. Opisana kružnica trokuta  i kružnica
i kružnica  polumjera
polumjera 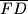 sa središtem u točki
sa središtem u točki  sijeku se u točkama
sijeku se u točkama  i
i  .
.
Dokažite da je dužina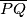 promjer kružnice
promjer kružnice  .
.
 unutar šiljastokutnog trokuta
unutar šiljastokutnog trokuta  takva da je pravac
takva da je pravac  zajednička tangenta kružnica opisanih trokutima
zajednička tangenta kružnica opisanih trokutima 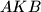 i
i 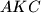 . Neka je točka
. Neka je točka  sjecište pravaca
sjecište pravaca 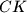 i
i  te neka je točka
te neka je točka  sjecište pravaca
sjecište pravaca 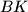 i
i  . Neka je točka
. Neka je točka  sjecište pravca
sjecište pravca  i simetrale dužine
i simetrale dužine 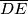 . Opisana kružnica trokuta
. Opisana kružnica trokuta  i kružnica
i kružnica  polumjera
polumjera 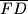 sa središtem u točki
sa središtem u točki  sijeku se u točkama
sijeku se u točkama  i
i  .
.Dokažite da je dužina
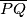 promjer kružnice
promjer kružnice  .
. Izraz 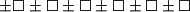 je napisan na ploči. Dva igrača,
je napisan na ploči. Dva igrača,  i
i  , igraju igru, naizmjence povlačeći poteze. Igrač
, igraju igru, naizmjence povlačeći poteze. Igrač  povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak
povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak  nekim prirodnim brojem. Nakon što su svi znakovi
nekim prirodnim brojem. Nakon što su svi znakovi  zamijenjeni, igrač
zamijenjeni, igrač  zamjenjuje svaki od predznaka
zamjenjuje svaki od predznaka 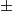 s jednim od predznaka
s jednim od predznaka  ili
ili  . Igrač
. Igrač  pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva
pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva 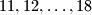 . U protivnome pobjeđuje igrač
. U protivnome pobjeđuje igrač  .
.
Koji igrač ima pobjedničku strategiju?
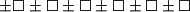 je napisan na ploči. Dva igrača,
je napisan na ploči. Dva igrača,  i
i  , igraju igru, naizmjence povlačeći poteze. Igrač
, igraju igru, naizmjence povlačeći poteze. Igrač  povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak
povlači prvi potez. U svakom potezu, igrač koji je na potezu zamjenjuje jedan znak  nekim prirodnim brojem. Nakon što su svi znakovi
nekim prirodnim brojem. Nakon što su svi znakovi  zamijenjeni, igrač
zamijenjeni, igrač  zamjenjuje svaki od predznaka
zamjenjuje svaki od predznaka 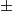 s jednim od predznaka
s jednim od predznaka  ili
ili  . Igrač
. Igrač  pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva
pobjeđuje ako vrijednost izraza na ploči nije djeljiva ni s jednim od brojeva 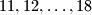 . U protivnome pobjeđuje igrač
. U protivnome pobjeđuje igrač  .
.Koji igrač ima pobjedničku strategiju?
 Školjka
Školjka  pozitivni realni brojevi takvi da vrijedi
pozitivni realni brojevi takvi da vrijedi 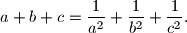 Dokaži
Dokaži ![2(a + b + c) \geq \sqrt[3]{7a^2b + 1} + \sqrt[3]{7b^2c + 1} + \sqrt[3]{7c^2a + 1} \text{.}](/media/m/b/d/5/bd5f82834e8a41edd87111ad765bc5c5.png) Nađi sve trojke
Nađi sve trojke 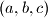 za koje vrijedi jednakost.
za koje vrijedi jednakost. 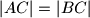 . Neka je
. Neka je  točka unutar tog trokuta takva da je
točka unutar tog trokuta takva da je 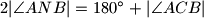 . Neka je
. Neka je 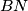 i pravca paralelnog pravcu
i pravca paralelnog pravcu 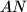 koji prolazi točkom
koji prolazi točkom  . Neka je
. Neka je 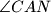 i simetrale
i simetrale 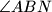 .
.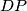 i
i  i
i  prirodni brojevi. Dokaži da postoje prirodni brojevi
prirodni brojevi. Dokaži da postoje prirodni brojevi  i
i  takvi da vrijedi
takvi da vrijedi 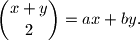
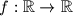 takve da je
takve da je 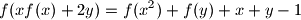 za sve
za sve 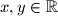 .
. 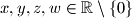 takvi da je
takvi da je 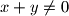 ,
, 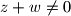 i
i 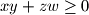 . Dokažite nejednakost
. Dokažite nejednakost 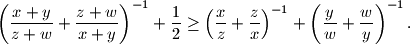
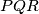 takav da je
takav da je 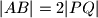 ,
, 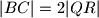 ,
, 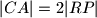 , a pravci
, a pravci  ,
, 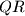 i
i 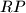 prolaze točkama
prolaze točkama 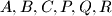 su međusobno različite.)
su međusobno različite.) 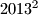 napisani su redak po redak u tablicu koja se sastoji od
napisani su redak po redak u tablicu koja se sastoji od 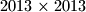 polja. Nakon toga, istovremeno su izbrisani svi retci i svi stupci koji sadržavaju barem jedan od potpunih kvadrata
polja. Nakon toga, istovremeno su izbrisani svi retci i svi stupci koji sadržavaju barem jedan od potpunih kvadrata  .
.