Europski matematički kup
 i točka
i točka  na simetrali kuta
na simetrali kuta  . Kružnica
. Kružnica  opisana trokutu
opisana trokutu 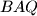 siječe stranicu
siječe stranicu  u točki
u točki 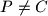 . Kružnica
. Kružnica  opisana je trokutu
opisana je trokutu 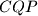 . Radijus kružnice
. Radijus kružnice  je veći od radijusa kružnice
je veći od radijusa kružnice  . Kružnica sa središtem u
. Kružnica sa središtem u  i radijusom
i radijusom 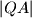 siječe kružnicu
siječe kružnicu  u točkama
u točkama  i
i  . Kružnica sa središtem u
. Kružnica sa središtem u  i radijusom
i radijusom 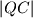 siječe kružnicu
siječe kružnicu  u točkama
u točkama  i
i  . Dokaži da je
. Dokaži da je 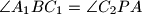 .
.  prirodan broj. Na Europskom šahovskom kupu sudjelovalo je nekoliko igrača. Svaka dva igrača su odigrala točno jednu partiju u kojoj je netko pobijedio (nije bilo remija). Ustanovljeno je da je za svakih
prirodan broj. Na Europskom šahovskom kupu sudjelovalo je nekoliko igrača. Svaka dva igrača su odigrala točno jednu partiju u kojoj je netko pobijedio (nije bilo remija). Ustanovljeno je da je za svakih  igrača bilo moguće naći igrača koji ih je sve pobijedio. Također je ustanovljeno da je broj igrača na turniru bio najmanji mogući za takav
igrača bilo moguće naći igrača koji ih je sve pobijedio. Također je ustanovljeno da je broj igrača na turniru bio najmanji mogući za takav  . Je li moguće da su na svečanoj večeri svi igrači bili smješteni za okrugli stol tako da je svatko sjedio pored igrača kojeg je pobijedio i pored igrača od kojeg je izgubio?
. Je li moguće da su na svečanoj večeri svi igrači bili smješteni za okrugli stol tako da je svatko sjedio pored igrača kojeg je pobijedio i pored igrača od kojeg je izgubio?  i točka
i točka  unutar njega. Pravac paralelan s
unutar njega. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Pravac paralelan s
redom. Pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i 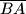 u točkama
u točkama  i
i  redom, dok pravac paralelan s
redom, dok pravac paralelan s  koji prolazi kroz
koji prolazi kroz  siječe stranice
siječe stranice  i
i  u točkama
u točkama  i
i  redom. Dokaži da vrijedi
redom. Dokaži da vrijedi  gdje
gdje  i
i  označavaju površinu trokuta
označavaju površinu trokuta 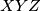 , odnosno površinu četverokuta
, odnosno površinu četverokuta  .
.  kotačića na kojima su zapisane znamenke
kotačića na kojima su zapisane znamenke 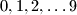 tim redom (nakon
tim redom (nakon  opet dolazi
opet dolazi  ). Točno jedna šifra otključava taj lokot. Jedan potez sastoji se od okretanja jednog od kotačića za jednu znamenku u bilo kojem smjeru, te se lokot odmah otvara ukoliko je novodobivena kombinacija jednaka šifri. Na početku su kotačići okrenuti tako da pokazuju kombinaciju
). Točno jedna šifra otključava taj lokot. Jedan potez sastoji se od okretanja jednog od kotačića za jednu znamenku u bilo kojem smjeru, te se lokot odmah otvara ukoliko je novodobivena kombinacija jednaka šifri. Na početku su kotačići okrenuti tako da pokazuju kombinaciju 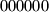 , te je provjereno da ta kombinacija ne otvara lokot.
, te je provjereno da ta kombinacija ne otvara lokot.a) Koji je najmanji broj poteza koji nam je potreban da sigurno otkrijemo šifru?
b) Koji je najmanji broj poteza koji nam je potreban da sigurno otkrijemo šifru, ako nam je još na početku rečeno da nijedna od kombinacija
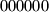 ,
, 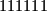 ,
, 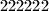 ,
,  ,
, 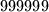 nije šifra za taj lokot?
nije šifra za taj lokot?  znamenaka jedan ili nula zovemo kodom. Podniz koda je palindrom ako se jednako čita s lijeva na desno i s desna na lijevo. Palindrom zovemo lijepim ako se njegove znamenke u kodu pojavljuju za redom. (Kod
znamenaka jedan ili nula zovemo kodom. Podniz koda je palindrom ako se jednako čita s lijeva na desno i s desna na lijevo. Palindrom zovemo lijepim ako se njegove znamenke u kodu pojavljuju za redom. (Kod 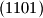 sadrži 10 palindroma, od kojih je 6 lijepih.)
sadrži 10 palindroma, od kojih je 6 lijepih.)a) Koji je najmanji mogući broj palindroma u kodu?
b) Koji je najmanji mogući broj lijepih palindroma u kodu?
Dana je ploča  , čiji su retci numerirani brojevima od
, čiji su retci numerirani brojevima od  do
do  odozgo prema dolje i stupci brojevima od
odozgo prema dolje i stupci brojevima od  do
do  s lijeva na desno. U svakom polju ploče s koordinatama
s lijeva na desno. U svakom polju ploče s koordinatama  napisan je broj
napisan je broj 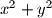 . Na početku nam je dana figura i možemo je postaviti na proizvoljno polje ploče. Nakon toga, u svakom potezu možemo pomaknuti figuru na neko drugo polje ukoliko to polje već nije bilo posjećeno i ako je zadovoljen barem jedan od dva sljedeća uvjeta:
. Na početku nam je dana figura i možemo je postaviti na proizvoljno polje ploče. Nakon toga, u svakom potezu možemo pomaknuti figuru na neko drugo polje ukoliko to polje već nije bilo posjećeno i ako je zadovoljen barem jedan od dva sljedeća uvjeta:  Mogu li sva polja ploče biti posjećena ako je
Mogu li sva polja ploče biti posjećena ako je
a) 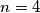 ,
,
b) 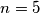 ?
?
(Josip Pupić)
Grupa matematičara nalazi se na konferenciji. Kažemo da je matematičar  -zadovoljan ako je u prostoriji s barem još
-zadovoljan ako je u prostoriji s barem još  ljudi kojima se on divi ili je u prostoriji s barem
ljudi kojima se on divi ili je u prostoriji s barem  ljudi koji se dive njemu. Poznato je da su svi matematičari na konferenciji
ljudi koji se dive njemu. Poznato je da su svi matematičari na konferenciji 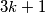 -zadovoljni, ukoliko se svi nalaze u jednoj sobi prostoriji. Dokaži da je sve matematičare moguće podijeliti u dvije prostorije tako da nikoja prostorija nije prazna i tako da svi matematičari barem
-zadovoljni, ukoliko se svi nalaze u jednoj sobi prostoriji. Dokaži da je sve matematičare moguće podijeliti u dvije prostorije tako da nikoja prostorija nije prazna i tako da svi matematičari barem  -zadovoljni. Diviti se nekome nije uzajamna relacija. Nitko se ne divi samome sebi.
-zadovoljni. Diviti se nekome nije uzajamna relacija. Nitko se ne divi samome sebi.
(Matija Bucić)
Skakavac skaže po brojevnom pravcu. Na početku se nalazi u ishodištu. U  -tom skoku duljina njegovog skoka je
-tom skoku duljina njegovog skoka je  .
.
a) Ako je duljina skoka paran broj, tada skače u lijevo, inače skače u desno (primjerice, u prvom koraku skače jedan korak udesno, u drugom dva koraka ulijevo, u trećem tri koraka udesno, u četvrtom četiri koraka ulijevo...). Hoće li skakavac posjetiti svaki cijeli broj barem jednom?
b) Ako je duljina skoka broj djeljiv s tri, tada skače u lijevo, inače skače u desno (primjerice, u prvom koraku skače jedan korak udesno, u drugom dva koraka udesno, u trećem tri koraka ulijevo, u četvrtom četiri koraka udesno...). Hoće li skakavac posjetiti svaki cijeli broj barem jednom?
(Matko Ljulj)
Kružnice  i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Neka su točke
. Neka su točke 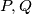 na kružnicama
na kružnicama 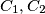 redom tako da vrijedi
redom tako da vrijedi 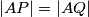 . Dužina
. Dužina 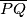 siječe kružnice
siječe kružnice  i
i  u točkama
u točkama 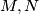 redom. Neka je
redom. Neka je  polovište kružnog luka
polovište kružnog luka 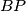 kružnice
kružnice  koji ne sadrži točku
koji ne sadrži točku  te neka je
te neka je  polovište kružnog luka
polovište kružnog luka 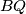 kružnice
kružnice  koji ne sadrži točku
koji ne sadrži točku  . Neka je
. Neka je  sjecište pravaca
sjecište pravaca 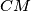 i
i 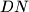 . Dokaži da je pravac
. Dokaži da je pravac  okomit na
okomit na  .
.
(Steve Dinh)
Par prirodnih brojeva 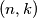 pri čemu je
pri čemu je  zovemo slatkim parom ako postoji tablica
zovemo slatkim parom ako postoji tablica  koja se sastoji od jedinica i nula i ima sljedeća svojstva:
koja se sastoji od jedinica i nula i ima sljedeća svojstva: 
Riješi dva sljedeća potproblema:
a) Neka je 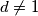 djelitelj broja
djelitelj broja  . Odredi sve moguće ostatke broja
. Odredi sve moguće ostatke broja  pri dijeljenju sa
pri dijeljenju sa  .
.
b) Dokaži da postoji beskonačno mnogo slatkih parova.
(Miroslav Marinov, Daniel Atanasov)
Za neka dva prirodna broja  i
i  , Ivica i Marica igraju sljedeću igru: Za dane hrpe od
, Ivica i Marica igraju sljedeću igru: Za dane hrpe od  i
i  keksa, u svakom potezu igrač uzima
keksa, u svakom potezu igrač uzima  keksa s jedne hrpe, pojede ih
keksa s jedne hrpe, pojede ih  , te ostalih
, te ostalih  vrati na drugu hrpu. Prirodan broj
vrati na drugu hrpu. Prirodan broj  je proizvoljan u svakom potezu. Igrači igraju naizmjence, s time da Ivica igra prvi. Igrač koji ne može napraviti potez, gubi igru. Pretpostavljajući da oba igrača igraju optimalno, odredi sve parove brojeva
je proizvoljan u svakom potezu. Igrači igraju naizmjence, s time da Ivica igra prvi. Igrač koji ne može napraviti potez, gubi igru. Pretpostavljajući da oba igrača igraju optimalno, odredi sve parove brojeva 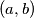 za koje Marica ima pobjedničku strategiju.
za koje Marica ima pobjedničku strategiju.
(Petar Orlić)
 Školjka
Školjka  skup prirodnih brojeva takav da za svaka dva elementa
skup prirodnih brojeva takav da za svaka dva elementa 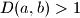 , a za svaka tri elementa tog skupa
, a za svaka tri elementa tog skupa  vrijedi
vrijedi 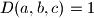 . Je li moguće da
. Je li moguće da 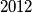 članova?
članova?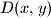 , odnosno
, odnosno 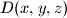 označava najveći zajednički djelitelj brojeva
označava najveći zajednički djelitelj brojeva 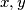 , odnosno brojeva
, odnosno brojeva 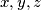 .)
.)  ,
,  i
i  takvi da je
takvi da je 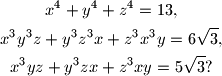
 koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 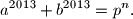
 . Dužine
. Dužine 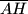 i
i 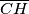 sijeku dužine
sijeku dužine 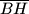 i
i 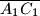 , a
, a 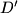 osnosimetrična slika točke
osnosimetrična slika točke  . Dokaži da je četverokut
. Dokaži da je četverokut 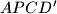 tetivan.
tetivan.  i
i  :
: ![\sqrt[3]{\frac{abc}{a+b+d}}+\sqrt[3]{\frac{def}{c+e+f}} < \sqrt[3]{(a+b+d)(c+e+f)} \text{.}](/media/m/4/c/5/4c5c85615e39c0b91633ab9b3531da60.png)
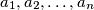 strogo manjih od
strogo manjih od 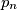 , gdje
, gdje 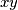 . Ako se pojave dva jednaka broja Oleg pobjeđuje. Može li Oleg garantirati pobjedu?
. Ako se pojave dva jednaka broja Oleg pobjeđuje. Može li Oleg garantirati pobjedu?  neka je
neka je 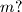 umnožak prvih
umnožak prvih 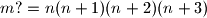 .
.  pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 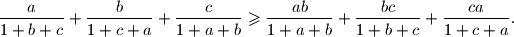
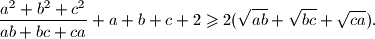
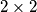 .
.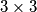 .
.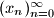 definiranom sa
definiranom sa 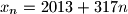 nalazi beskonačno mnogo prirodnih brojeva čiji su decimalni zapisi palindromi.
nalazi beskonačno mnogo prirodnih brojeva čiji su decimalni zapisi palindromi. 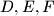 nožišta visina iz
nožišta visina iz 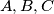 redom. Neka su
redom. Neka su 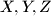 polovišta visina
polovišta visina 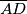 ,
, 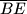 ,
, 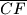 redom. Dokaži da se okomica iz
redom. Dokaži da se okomica iz 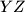 , okomica iz
, okomica iz 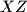 te okomica iz
te okomica iz  sijeku u jednoj točki.
sijeku u jednoj točki. 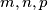 sa svojstvom
sa svojstvom 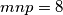 . U ovisnosti o tim konstantama nađi minimum izraza
. U ovisnosti o tim konstantama nađi minimum izraza 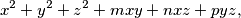 gdje su
gdje su 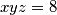 . Kada se postiže jednakost?
. Kada se postiže jednakost?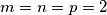 ,
,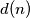 označava broj pozitivnih djelitelja broja
označava broj pozitivnih djelitelja broja  na sljedeći način:
na sljedeći način: 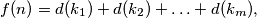 gdje su
gdje su 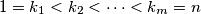 svi djelitelji broja
svi djelitelji broja 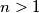 zovemo skoro savršenim ako je
zovemo skoro savršenim ako je 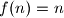 . Nađi sve skoro savršene brojeve.
. Nađi sve skoro savršene brojeve.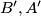 točke na simetralama dužina
točke na simetralama dužina 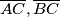 redom takve da je
redom takve da je 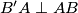 i
i 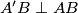 . Neka je
. Neka je  središte opisane kružnice trokutu
središte opisane kružnice trokutu 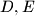 točke na pravcima
točke na pravcima 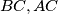 redom takve da je
redom takve da je 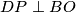 i
i 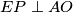 . Neka je
. Neka je 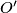 središte opisane kružnice trokuta
središte opisane kružnice trokuta 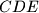 . Dokaži da su točke
. Dokaži da su točke 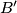 ,
, 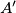 i
i 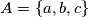 tročlani podskup skupa prirodnih brojeva. Dokaži da postoji podskup
tročlani podskup skupa prirodnih brojeva. Dokaži da postoji podskup 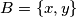 skupa
skupa 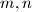 izraz
izraz 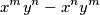 djeljiv s
djeljiv s  .
.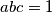 . Dokaži da je
. Dokaži da je 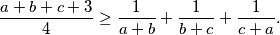
 i
i 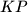 paralelan s težišnicom trokuta
paralelan s težišnicom trokuta 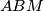 povučenom iz točke
povučenom iz točke 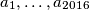 prirodnih brojeva takvih da je svaka suma
prirodnih brojeva takvih da je svaka suma 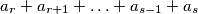 (uz
(uz 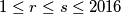 ) složen broj, no
) složen broj, no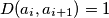 za sve
za sve 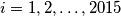 ;
;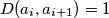 za sve
za sve 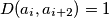 za sve
za sve 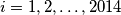 ?
?