Let 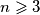 be an integer. A labelling of the
be an integer. A labelling of the  vertices, the
vertices, the  sides and the interior of a regular
sides and the interior of a regular  -gon by
-gon by 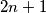 distinct integers is called memorable if the following conditions hold:
distinct integers is called memorable if the following conditions hold:
(a) Each side has a label that is the arithmetic mean of the labels of its endpoints.
(b) The interior of the  -gon has a label that is the arithmetic mean of the labels of all the vertices.
-gon has a label that is the arithmetic mean of the labels of all the vertices.
Determine all integers 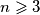 for which there exists a memorable labelling of a regular
for which there exists a memorable labelling of a regular  -gon consisting of
-gon consisting of 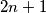 consecutive integers.
consecutive integers.
Let 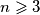 be an integer. A sequence
be an integer. A sequence 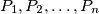 of distinct points in the plane is called good if no three of them are collinear, the polyline
of distinct points in the plane is called good if no three of them are collinear, the polyline 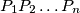 is non-self-intersecting and the triangle
is non-self-intersecting and the triangle 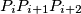 is oriented counterclockwise for every
is oriented counterclockwise for every 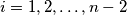 . For every integer
. For every integer 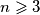 determine the greatest possible integer
determine the greatest possible integer  with the following property: there exist
with the following property: there exist  distinct points
distinct points 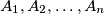 in the plane for which there are
in the plane for which there are  distinct permutations
distinct permutations 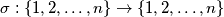 such that
such that 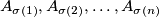 is good.
is good.
(A polyline 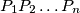 consists of the segments
consists of the segments 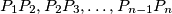 .)
.)
Let  be an acute-angled triangle with
be an acute-angled triangle with  and circumcircle
and circumcircle  . Let
. Let  be the midpoint of the shorter arc
be the midpoint of the shorter arc  of
of  , and let
, and let  be the intersection of the rays
be the intersection of the rays  and
and 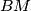 . Let
. Let 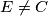 be the intersection of the internal bisector of the angle
be the intersection of the internal bisector of the angle 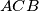 and the circumcircle of the triangle
and the circumcircle of the triangle 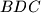 . Let us assume that
. Let us assume that  is inside the triangle
is inside the triangle  and there is an intersection
and there is an intersection  of the line
of the line 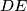 and the circle
and the circle  such that
such that  is the midpoint of the segment
is the midpoint of the segment 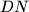 .
.
Show that  is the midpoint of the segment
is the midpoint of the segment 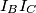 , where
, where 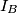 and
and 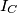 are the excentres of
are the excentres of  opposite to
opposite to  and
and  , respectively.
, respectively.
 Školjka
Školjka  satisfying
satisfying 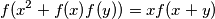 for all real numbers
for all real numbers  and
and  .
. 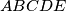 be a convex pentagon. Let
be a convex pentagon. Let  be the intersection of the lines
be the intersection of the lines 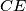 and
and  . Assume that
. Assume that 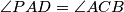 and
and 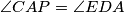 .
. 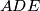 are collinear with
are collinear with 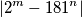 where
where  and
and 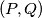 with real coefficients satisfying
with real coefficients satisfying 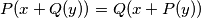 for all real numbers
for all real numbers 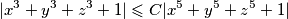 holds for all real numbers
holds for all real numbers 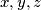 satisfying
satisfying 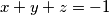 .
.  board. Each lamp is either on or off. A lamp is called bad if it has an even number of neighbours that are on. What is the smallest possible number of bad lamps on such a board?
board. Each lamp is either on or off. A lamp is called bad if it has an even number of neighbours that are on. What is the smallest possible number of bad lamps on such a board?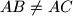 , circumcentre
, circumcentre  and circumcircle
and circumcircle 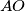 intersect
intersect  meet
meet 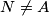 . Finally, let
. Finally, let 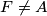 be a point on
be a point on 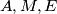 and
and  are concyclic.
are concyclic. 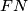 bisects the segment
bisects the segment  .
.  such that there exists a permutation
such that there exists a permutation 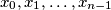 of the numbers
of the numbers 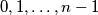 with the property that the
with the property that the 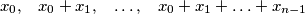 are pairwise distinct modulo
are pairwise distinct modulo 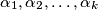 as the sequence of exponents in the prime factorization of
as the sequence of exponents in the prime factorization of 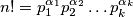 , where
, where 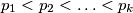 are primes. Determine all integers
are primes. Determine all integers  for which
for which