Općinsko natjecanje 1995 SŠ4 1
Dodao/la:
arhiva2. travnja 2012. Za broj
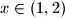
definiran je niz
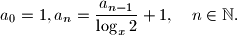
Dokažite da je
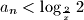
za svaki

.
%V0
Za broj $x \in (1, 2)$ definiran je niz $$a_{0} = 1, a_{n} = \frac{a_{n-1}}{\log _{x}2} + 1 ,\quad n \in \mathbb{N}.
$$ Dokažite da je $a_{n} < \log _{\frac{2}{x}}2$ za svaki $n \in \mathbb{N}$.
Izvor: Općinsko natjecanje iz matematike 1995