Državno natjecanje 2000 SŠ3 4
Dodao/la:
arhiva1. travnja 2012. Dokažite da za svaki prirodan broj

vrijedi ova jednakost
![\lfloor \log_{2}{n} \rfloor + \lfloor \log_{3}{n} \rfloor + \ldots + \lfloor \log_{n}{n} \rfloor = \lfloor \sqrt{n} \rfloor + \lfloor \sqrt[3]{n} \rfloor + \ldots + \lfloor \sqrt[n]{n} \rfloor.](/media/m/f/1/a/f1a92a85065e9a07ee5647bb30b974e5.png)
(
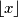
je oznaka za najveći cijeli broj koji nije veći od

.)
%V0
Dokažite da za svaki prirodan broj $n \geq 2$ vrijedi ova jednakost
$$\lfloor \log_{2}{n} \rfloor + \lfloor \log_{3}{n} \rfloor + \ldots + \lfloor \log_{n}{n} \rfloor = \lfloor \sqrt{n} \rfloor + \lfloor \sqrt[3]{n} \rfloor + \ldots + \lfloor \sqrt[n]{n} \rfloor.$$
( $\lfloor x \rfloor$ je oznaka za najveći cijeli broj koji nije veći od $x$.)
Izvor: Državno natjecanje iz matematike 2000