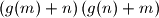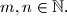Each of the six boxes  ,
,  ,
, 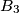 ,
, 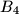 ,
, 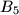 ,
, 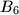 initially contains one coin. The following operations are allowed
initially contains one coin. The following operations are allowed
Type 1) Choose a non-empty box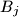 ,
, 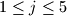 , remove one coin from
, remove one coin from 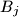 and add two coins to
and add two coins to 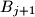 ;
;
Type 2) Choose a non-empty box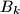 ,
, 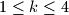 , remove one coin from
, remove one coin from 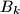 and swap the contents (maybe empty) of the boxes
and swap the contents (maybe empty) of the boxes 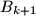 and
and 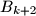 .
.
Determine if there exists a finite sequence of operations of the allowed types, such that the five boxes ,
,  ,
, 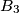 ,
, 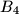 ,
, 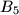 become empty, while box
become empty, while box 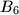 contains exactly
contains exactly 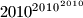 coins.
coins.
Proposed by Hans Zantema, Netherlands
 ,
,  ,
, 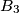 ,
, 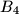 ,
, 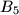 ,
, 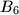 initially contains one coin. The following operations are allowed
initially contains one coin. The following operations are allowedType 1) Choose a non-empty box
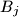 ,
, 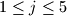 , remove one coin from
, remove one coin from 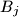 and add two coins to
and add two coins to 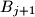 ;
; Type 2) Choose a non-empty box
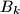 ,
, 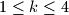 , remove one coin from
, remove one coin from 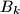 and swap the contents (maybe empty) of the boxes
and swap the contents (maybe empty) of the boxes 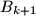 and
and 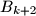 .
.Determine if there exists a finite sequence of operations of the allowed types, such that the five boxes
 ,
,  ,
, 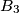 ,
, 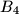 ,
, 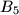 become empty, while box
become empty, while box 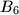 contains exactly
contains exactly 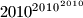 coins.
coins.Proposed by Hans Zantema, Netherlands
 Školjka
Školjka 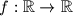 such that for all
such that for all 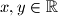 the following equality holds
the following equality holds 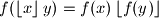
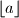 is greatest integer not greater than
is greatest integer not greater than 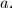
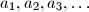 be a sequence of positive real numbers, and
be a sequence of positive real numbers, and  be a positive integer, such that
be a positive integer, such that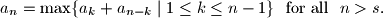
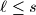 and
and  , such that
, such that 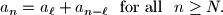
 be a point interior to triangle
be a point interior to triangle  (with
(with 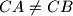 ). The lines
). The lines 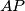 ,
, 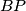 and
and 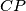 meet again its circumcircle
meet again its circumcircle  at
at  ,
,  , respectively
, respectively  . The tangent line at
. The tangent line at  to
to  at
at  . Show that from
. Show that from 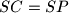 follows
follows 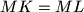 .
. as its incenter and
as its incenter and 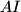 intersects
intersects  . Let
. Let  be a point on the arc
be a point on the arc 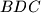 , and
, and  a point on the segment
a point on the segment  , such that
, such that 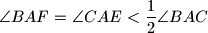 . If
. If  is the midpoint of
is the midpoint of 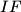 , prove that the meeting point of the lines
, prove that the meeting point of the lines 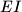 and
and 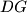 lies on
lies on 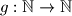 such that
such that