IMO Shortlist 2010 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Each of the six boxes 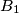 ,
, 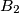 ,
, 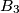 ,
, 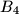 ,
, 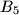 ,
, 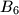 initially contains one coin. The following operations are allowed
initially contains one coin. The following operations are allowed
Type 1) Choose a non-empty box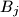 ,
, 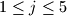 , remove one coin from
, remove one coin from 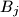 and add two coins to
and add two coins to 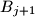 ;
;
Type 2) Choose a non-empty box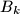 ,
, 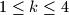 , remove one coin from
, remove one coin from 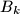 and swap the contents (maybe empty) of the boxes
and swap the contents (maybe empty) of the boxes 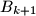 and
and 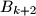 .
.
Determine if there exists a finite sequence of operations of the allowed types, such that the five boxes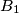 ,
, 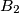 ,
, 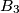 ,
, 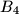 ,
, 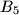 become empty, while box
become empty, while box 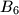 contains exactly
contains exactly 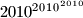 coins.
coins.
Proposed by Hans Zantema, Netherlands
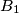 ,
, 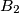 ,
, 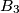 ,
, 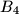 ,
, 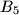 ,
, 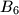 initially contains one coin. The following operations are allowed
initially contains one coin. The following operations are allowedType 1) Choose a non-empty box
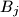 ,
, 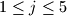 , remove one coin from
, remove one coin from 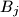 and add two coins to
and add two coins to 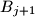 ;
; Type 2) Choose a non-empty box
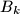 ,
, 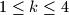 , remove one coin from
, remove one coin from 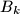 and swap the contents (maybe empty) of the boxes
and swap the contents (maybe empty) of the boxes 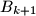 and
and 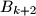 .
.Determine if there exists a finite sequence of operations of the allowed types, such that the five boxes
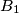 ,
, 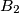 ,
, 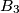 ,
, 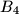 ,
, 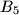 become empty, while box
become empty, while box 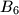 contains exactly
contains exactly 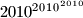 coins.
coins.Proposed by Hans Zantema, Netherlands
Izvor: Međunarodna matematička olimpijada, shortlist 2010
 Školjka
Školjka 
