Let  and
and  be positive integers with
be positive integers with 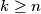 and
and  an even number. Let
an even number. Let  lamps labelled
lamps labelled  ,
,  , ...,
, ...,  be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
Let be the number of such sequences consisting of
be the number of such sequences consisting of  steps and resulting in the state where lamps
steps and resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off.
are all off.
Let be number of such sequences consisting of
be number of such sequences consisting of  steps, resulting in the state where lamps
steps, resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off, but where none of the lamps
are all off, but where none of the lamps  through
through  is ever switched on.
is ever switched on.
Determine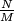 .
.
Author: Bruno Le Floch and Ilia Smilga, France
 and
and  be positive integers with
be positive integers with 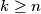 and
and  an even number. Let
an even number. Let  lamps labelled
lamps labelled  ,
,  , ...,
, ...,  be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on). Let
 be the number of such sequences consisting of
be the number of such sequences consisting of  steps and resulting in the state where lamps
steps and resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off.
are all off. Let
 be number of such sequences consisting of
be number of such sequences consisting of  steps, resulting in the state where lamps
steps, resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off, but where none of the lamps
are all off, but where none of the lamps  through
through  is ever switched on.
is ever switched on. Determine
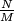 .
. Author: Bruno Le Floch and Ilia Smilga, France
Let  be a convex quadrilateral with
be a convex quadrilateral with 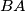 different from
different from  . Denote the incircles of triangles
. Denote the incircles of triangles  and
and 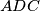 by
by 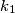 and
and 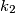 respectively. Suppose that there exists a circle
respectively. Suppose that there exists a circle  tangent to ray
tangent to ray 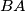 beyond
beyond  and to the ray
and to the ray  beyond
beyond  , which is also tangent to the lines
, which is also tangent to the lines  and
and  .
.
Prove that the common external tangents to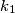 and
and 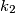 intersects on
intersects on  .
.
Author: Vladimir Shmarov, Russia
 be a convex quadrilateral with
be a convex quadrilateral with 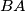 different from
different from  . Denote the incircles of triangles
. Denote the incircles of triangles  and
and 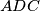 by
by 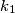 and
and 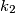 respectively. Suppose that there exists a circle
respectively. Suppose that there exists a circle  tangent to ray
tangent to ray 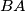 beyond
beyond  and to the ray
and to the ray  beyond
beyond  , which is also tangent to the lines
, which is also tangent to the lines  and
and  .
. Prove that the common external tangents to
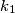 and
and 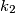 intersects on
intersects on  .
. Author: Vladimir Shmarov, Russia
 Školjka
Školjka 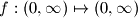 (so
(so  is a function from the positive real numbers) such that
is a function from the positive real numbers) such that 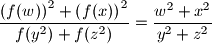
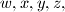 satisfying
satisfying 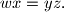
 ,
,  and
and  are three real numbers, all different from
are three real numbers, all different from 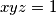 , then prove that
, then prove that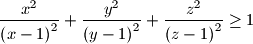 .
. 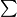 sign for cyclic summation, this inequality could be rewritten as
sign for cyclic summation, this inequality could be rewritten as 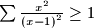 .)
.)  be the orthocenter of an acute-angled triangle
be the orthocenter of an acute-angled triangle 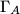 centered at the midpoint of
centered at the midpoint of 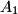 and
and 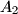 . Similarly, define the points
. Similarly, define the points 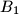 ,
, 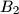 ,
, 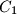 and
and 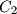 .
. 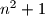 has a prime divisor greater than
has a prime divisor greater than 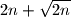 .
.