In a mathematical competition, in which 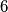 problems were posed to the participants, every two of these problems were solved by more than
problems were posed to the participants, every two of these problems were solved by more than  of the contestants. Moreover, no contestant solved all the
of the contestants. Moreover, no contestant solved all the 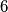 problems. Show that there are at least
problems. Show that there are at least  contestants who solved exactly
contestants who solved exactly  problems each.
problems each.
Radu Gologan and Dan Schwartz
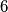 problems were posed to the participants, every two of these problems were solved by more than
problems were posed to the participants, every two of these problems were solved by more than  of the contestants. Moreover, no contestant solved all the
of the contestants. Moreover, no contestant solved all the 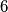 problems. Show that there are at least
problems. Show that there are at least  contestants who solved exactly
contestants who solved exactly  problems each.
problems each. Radu Gologan and Dan Schwartz
Let  be a fixed convex quadrilateral with
be a fixed convex quadrilateral with 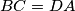 and
and  not parallel with
not parallel with 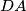 . Let two variable points
. Let two variable points  and
and  lie of the sides
lie of the sides  and
and 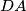 , respectively and satisfy
, respectively and satisfy 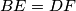 . The lines
. The lines  and
and  meet at
meet at  , the lines
, the lines  and
and  meet at
meet at  , the lines
, the lines  and
and  meet at
meet at  .
.
Prove that the circumcircles of the triangles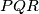 , as
, as  and
and  vary, have a common point other than
vary, have a common point other than  .
.
 be a fixed convex quadrilateral with
be a fixed convex quadrilateral with 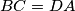 and
and  not parallel with
not parallel with 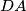 . Let two variable points
. Let two variable points  and
and  lie of the sides
lie of the sides  and
and 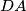 , respectively and satisfy
, respectively and satisfy 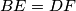 . The lines
. The lines  and
and  meet at
meet at  , the lines
, the lines  and
and  meet at
meet at  , the lines
, the lines  and
and  meet at
meet at  .
. Prove that the circumcircles of the triangles
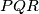 , as
, as  and
and  vary, have a common point other than
vary, have a common point other than  .
.  Školjka
Školjka 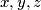 be three positive reals such that
be three positive reals such that 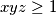 . Prove that
. Prove that 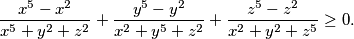
 :
:  ,
,  on
on  ,
,  on
on  and
and  ,
, 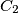 on
on  , such that they are the vertices of a convex hexagon
, such that they are the vertices of a convex hexagon 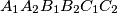 with equal side lengths.
with equal side lengths. 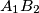 ,
, 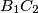 and
and 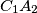 are concurrent.
are concurrent. 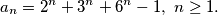
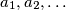 be a sequence of integers with infinitely many positive and negative terms. Suppose that for every positive integer
be a sequence of integers with infinitely many positive and negative terms. Suppose that for every positive integer  the numbers
the numbers 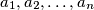 leave
leave